【题目】点D,E分别在△ABC的边AC,BD上,BD,CE交于点F,连接AF,∠FAE=∠FAD,FE=FD.
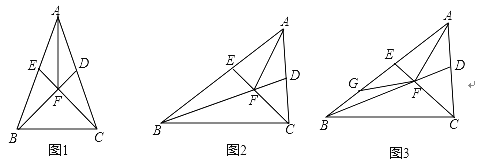
(1)如图1,若∠AEF=∠ADF,求证:AE=AD;
(2)如图2,若∠AEF≠∠ADF,FB平分∠ABC,求∠BAC的度数;
(3)在(2)的条件下,如图3,点G在BE上,∠CFG=∠AFB若AG=6,△ABC的周长为20,求BC长.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△AEF≌△ADF,根据全等三角形的对应边相等证明结论;
(2)过点F分别作AB,BC,AC边上的高,根据角平分线的性质定理得到FP=FQ,FP=FN,根据角平分线的判定定理得到CF平分∠ACB,证明Rt△PEF≌Rt△NDF,根据全等三角形的性质得到∠PEF=∠FDN,计算得到答案;
(3)在BC上取点R,使CR=CA,分别证明△CAF≌△CRF、△BGF≌△BRF,根据全等三角形的性质、三角形的周长公式计算即可.
(1)∵![]() ,
,![]() ,
,![]() .
.
∴![]() ,∴
,∴![]() .
.

(2)过![]() 点分别作
点分别作![]() ,
,![]() ,
,![]() 边上的高,
边上的高,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 为垂足.
为垂足.
∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,![]() ,∴
,∴![]() 平分
平分![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]()
![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
∴![]() 且
且![]() ,
,
∴![]() .
.
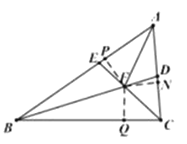
(3)在![]() 上取点
上取点![]() ,使
,使![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .
.
∵![]()
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单位为了解3500名党员职工每月党费上交情况,从中随机抽取50名党员职工,根据每月每名党员职工的党费情况给制如图所示的条形统计图.
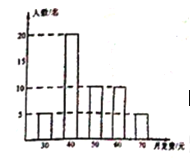
(1)求50名党职工每月觉费的平均数;
(2)直接写出这50名党员职工每月党费的众数与中位数;
(3)根据这50名党员职工每月党费的平均数,请你估计该单位3500名党员职工每月约上交党费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.

(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收
 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量. -
科目: 来源: 题型:
查看答案和解析>>【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
-
科目: 来源: 题型:
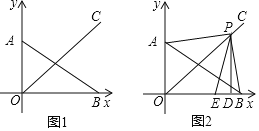
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,纵坐标为a的点A在y轴上,横坐标为b的点B在x轴上,实数a,b满足|a+b﹣8|+(3a﹣2b+1)2=0
(1)求a,b的值;
(2)如图1,第一象限的点P在∠AOB的平分线OC上,过点P作x轴的垂线,点D为垂足,设线段PD的长为d,△PAB的面积为S(S≠0)用含d的式子表示S,并直接写出相应的d的范围
(3)在(2)的条件下,如图2,当PA⊥PB时,点E在x轴上,连接PE,∠APE=2∠ABO,求PE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-4,
 ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=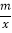 (m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连结PC、PD,若△PCA和△PDB面积相等,求点P的坐标.
相关试题

