【题目】如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2. 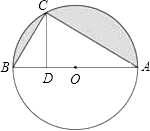
(1)求证:△ABC∽△ACD;
(2)求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠ACB,∠B+∠BAC=90°,∠DCA+∠CAB=90°,
∴∠B=∠ACD,
∴△ABC∽△ACD
(2)解:∵△ABC∽△ACD,
∴ ![]() =
= ![]() ,
,
∴AC2=ADAB=6×8=48,
∴CD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴S△ABC= ![]() ABCD=
ABCD= ![]() ×
× ![]() =8
=8 ![]() ,
,
∴S阴=S半圆﹣S△ABC=8 ![]() .
.

【解析】(1)根据两角对应相等的两个三角形相似即可证明.(2)先利用△ABC∽△ACD,得AC2=ADAB=48,再利用勾股定理求出CD,根据S阴=S半圆﹣S△ABC即可解决问题.
【考点精析】利用扇形面积计算公式和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生的特长爱好,提髙学生的综合素质,某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买2个竖笛和1个尤克里里共需290元;竖笛单价比尤克里里单价的一半少25元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共20个,但要求购买竖笛和尤克里里的总费用不超过3450元,则该校最多可以购买多少个尤克里里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图。(要求每位同学只能选择一种自己喜欢的球类;扇形统计图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数)请你根据图中提供的信息,解答下列问题:
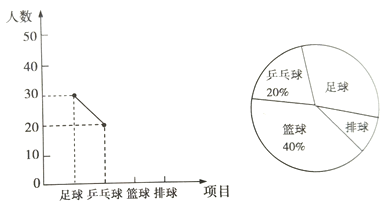
(1)在这次研究中,一共调查了多少名学生?
(2)喜欢排球的人数在扇形统计图中所对应的扇形的圆心角是多少度?
(3)补全频数分布折线统计图。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:
 =
=  .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
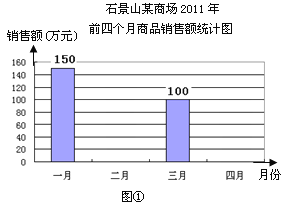
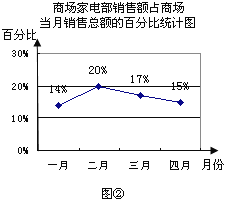
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须既不平行也不相交(其中n是正整数)。那么当黑、白两个甲壳虫各爬行完第2017条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )

A. 0 B. 1 C.
 D.
D. 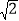
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=2x2﹣x﹣3.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象;
(2)根据图象直接回答:当x为何值时,y<0?当x为何值时y>﹣3?
相关试题

