Question

【题目】（1）问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：ADBC=APBP．

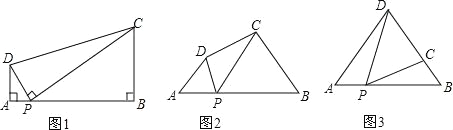
（2）探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．

（3）应用：请利用（1）（2）获得的经验解决问题：

如图3，在△ABD中，AB=12，AD=BD=10．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．

Answer 1

【答案】(1)证明见解析；（2）结果成立，理由见解析；（3）t的值为2秒或10秒．

【解析】

试题分析：（1）由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC，即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；

（2）由∠DPC=∠A=∠B=θ可得∠ADP=∠BPC，即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；

（3）过点D作DE⊥AB于点E，根据等腰三角形的性质可得AE=BE=6，根据勾股定理可得DE=8，由题可得DC=DE=8，则有BC=10-8=2．易证∠DPC=∠A=∠B．根据ADBC=APBP，就可求出t的值．

试题解析：（1）如图1，

∵∠DPC=∠A=∠B=90°，

∴∠ADP+∠APD=90°，

∠BPC+∠APD=90°，

∴∠APD=∠BPC，

∴△ADP∽△BPC，

∴，

∴ADBC=APBP；

（2）结论ADBC=APBP仍成立；

证明：如图2，∵∠BPD=∠DPC+∠BPC，

又∵∠BPD=∠A+∠APD，

∴∠DPC+∠BPC=∠A+∠APD，

∵∠DPC=∠A=θ，

∴∠BPC=∠APD，

又∵∠A=∠B=θ，

∴△ADP∽△BPC，

∴，

∴ADBC=APBP；

（3）如下图，过点D作DE⊥AB于点E，

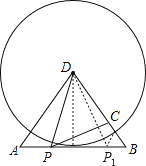
∵AD=BD=10，AB=12，

∴AE=BE=6

∴DE==8，

∵以D为圆心，以DC为半径的圆与AB相切，

∴DC=DE=8，

∴BC=10-8=2，

∵AD=BD，

∴∠A=∠B，

又∵∠DPC=∠A，

∴∠DPC=∠A=∠B，

由（1）（2）的经验得ADBC=APBP，

又∵AP=t，BP=12-t，

∴t（12-t）=10×2，

∴t=2或t=10，

∴t的值为2秒或10秒．