【题目】如图,△ABC和△ADE都是等边三角形,BD与CE相交于O.
(1)求证:BD=CE;
(2)OA平分∠BOE吗?说明理由.

参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据等边三角形的性质得到AB=AC,AD=AE,∠BAC=∠DAE=60°,则易得∠BAD=∠CAE,根据“SAS”有△BAD≌△CAE,利用全等三角形的性质即可得到结论;(2)、作AF⊥BD,AG⊥CE,垂足分别是F、G,由△BAD≌△CAE,根据全等三角形的性质有AF=AG,再根据角平分线的判定定理即可得到OA平分∠BOE.
试题解析:(1)、∵△ABC和△ADE都是等边三角形, ∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE, 在△BAD和△CAE中, 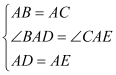 ,
,
∴△BAD≌△CAE(SAS), ∴BD=CE;
(2)、OA平分∠BOE.理由如下: 作AF⊥BD,AG⊥CE,垂足分别是F、G,如图,
∵AF、AG恰好是两个全等三角形△BAD与△CAE对应边上的高, ∴AF=AG, ∴OA平分∠BOE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】任意写出一个偶数和一个奇数,两数之和是奇数的概率是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“对顶角相等”的逆命题为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两条边长度分别为1和4,则第三边a可取_______.(填一个满足条件的数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD
 BC=AP
BC=AP BP.
BP.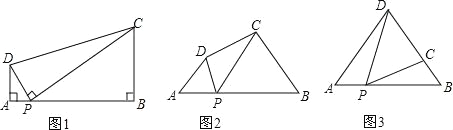
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=12,AD=BD=10.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
A. 37 B. 38 C. 40 D. 42
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形中,最小的角是30度,最短边长是5厘米,则斜边长为 .
相关试题

