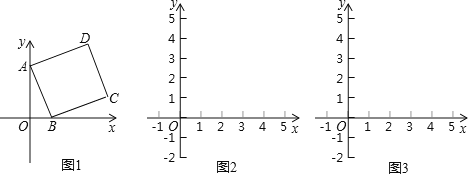
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
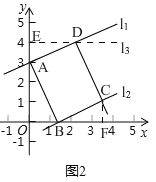
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
参考答案:
【答案】(1)m=1,n=3;(2)C(m+![]() ,1);(3)当m=
,1);(3)当m=![]() 时,矩形ABCD的对角线AC的长最短为4.
时,矩形ABCD的对角线AC的长最短为4.
【解析】
试题分析:(1)先判断出∠ADE=∠BAO,即可判断出△ABO≌△ADE,得出DE=OA=3,AE=OB,即可求出m;
(2)先根据垂直的作法即可画出图形,判断出△ADE≌△CBF,得出CF=1,再判断出△AOB∽△DEA,即可得出OB=![]() ,即可得出结论;
,即可得出结论;
(3)先判断出BD⊥x轴时,求出AC的最小值,再求出DM=2,最后用勾股定理求出AE即可得出m.
试题解析:(1)如图1,过点D作DE⊥y轴于E,
∴∠AED=∠AOB=90°,∴∠ADE+∠DAE=90°,
∵四边形ABCD是正方形,∴AD=AB,∠BAD=90°,
∴∠DAE+∠BAO=90°,∴∠ADE=∠BAO,
在△ABO和△ADE中,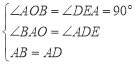 ,
,
∴△ABO≌△ADE,
∴DE=OA,AE=OB,
∵A(0,3),B(m,0),D(n,4),
∴OA=3,OB=m,OE=4,DE=n,∴n=3,
∴OE=OA+AE=OA+OB=3+m=4,∴m=1;
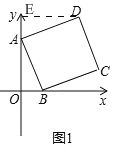
(2)画法:如图2,①过点A画AB的垂线l1,
过点B画AB的垂线l2,
②过点E(0,4),画y轴的垂线l3交l1于D,
③过点D画直线l1的垂线交直线l2于点C,
所以,四边形ABCD是所求作的图形,
过点C作CF⊥x轴于F,
∴∠CBF+∠BCF=90°,
∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠BAD=90°,
∴∠ABO+∠CBF=90°,∴∠BCF=∠ABO,同理:∠ABO=∠DAE,
∴∠BCF=∠DAE,
在△ADE和△CBF中,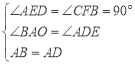 ,
,
∴△ADE≌△CBF,
∴DE=BF=n,AE=CF=1,
易证△AOB∽△DEA,∴![]() ,∴
,∴![]() ,∴n=
,∴n=![]() ,
,
∴OF=OB+BF=m+![]() ,∴C(m+
,∴C(m+![]() ,1);
,1);
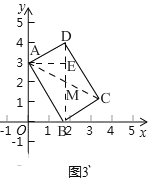
(3)如图3,由矩形的性质可知,BD=AC,
∴BD最小时,AC最小,
∵B(m,0),D(n,4),
∴当BD⊥x轴时,BD有最小值4,此时,m=n,
即:AC的最小值为4,
连接BD,AC交于点M,过点A作AE⊥BD于E,
由矩形的性质可知,DM=BM=![]() BD=2,
BD=2,
∵A(0,3),D(n,4),∴DE=1,∴EM=DM﹣DE=1,
在Rt△AEM中,根据勾股定理得,AE=![]() ,∴m=
,∴m=![]() ,即:
,即:
当m=![]() 时,矩形ABCD的对角线AC的长最短为4.
时,矩形ABCD的对角线AC的长最短为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:
(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标(用含a的代数式表示);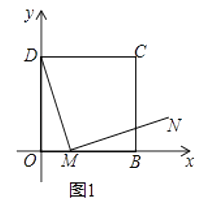
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.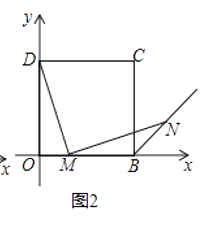
(3)如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.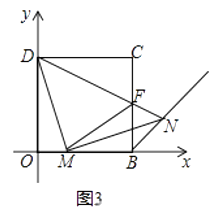
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣xy3)2的结果是( )
A.x2y6
B.﹣x2y6
C.x2y9
D.﹣x2y9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,AC与OB交于点D (8,4),反比例函数y=
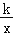 的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 2 .
的图象经过点D.若将菱形OABC向左平移n个单位,使点C落在该反比例函数图象上,则n的值为 2 .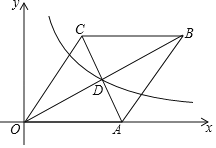
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
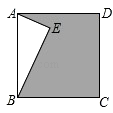
A.16
B.18
C.19
D.21 -
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A.44×108B.4.4×109C.4.4×108D.4.4×1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
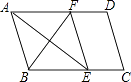
A.13
B.14
C.15
D.16
相关试题

