Question

【题目】如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．

（1）设△DPQ的面积为S，求S与t之间的关系式；

（2）当t为何值时，四边形PCDQ是平行四边形？

（3）分别求出当t为何值时，①PD=PQ；②DQ=PQ．

Answer 1

【答案】（1）S=-6t+96；（2）当t=5时，四边形PCDQ是平行四边形；（3）①当t=时，PD=PQ；②当t=时，DQ=PQ

【解析】

（1）S=DQAB，AQ=t，DQ=AD-AQ=16-t，将DQ和AB的长代入，可求出S与t之间的函数关系式；

（2）当四边形PCDQ为平行四边形时，PC=DQ，即16-t=21-2t，可将t求出；

（3）①当PD=PQ时，QE=ED=QD，DE=162t，AE=BP=AQ+QE，即2t=t+162t，从而可将t求出；

②当DQ=PQ时，根据DQ2=PQ2即：t2+122=（16-t）2可将t求出．

（1）在直角梯形ABCD中，AD∥BC，∠A=90°，BC=21，AB=12，AD=16，

设AQ=t，BP=2t，则DQ=16t，PC=212t，

过点P作PE⊥AD于E，

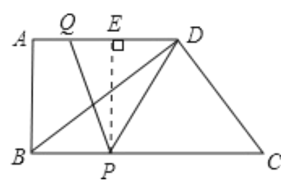
则四边形ABPE是矩形，PE=AB=12，

∴S=DQAB=(16t)×12=6t+96

故答案为：S=6t+96

（2）当四边形PCDQ是平行四边形时，PC=DQ，

∴212t=16t解得：t=5，

∴当t=5时，四边形PCDQ是平行四边形．

故答案为：当t=5时，四边形PCDQ是平行四边形

（3）∵AE=BP=2t，PE=AB=12，

①当PD=PQ时，QE=ED=QD，

∵DE=162t，

∴AE=BP=AQ+QE，即2t=t+162t，

解得：t=，

∴当t=时，PD=PQ

故答案为：当t=时，PD=PQ

②当DQ=PQ时，DQ2=PQ2

∴t2+122=(16t)2解得：t=

∴当t=时，DQ=PQ

故答案为：当t=时，DQ=PQ