【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

参考答案:
【答案】(1)∠C=60°.
(2)∠C-∠B=2∠DEF.理由见解析
【解析】试题分析:(1)已知:EF⊥BC,∠DEF=10°可以求得∠EDF的度数,∠EDF又是ABD的外角,已知∠B的度数,可求得∠BAD的值,AD平分∠BAC,所以∠BAC的值也可求出,从而求出∠C。(2)EF⊥BC,可得到∠EDF=90°-∠DEF,∠EDF又是ABD的外角,可得到∠BAD=∠EDF-∠B=90°-∠DEF-∠B,然后可将![]() BAC用含∠DEF、∠B的角来表示,即
BAC用含∠DEF、∠B的角来表示,即![]() BAC =2(90°-∠DEF-∠B),最后利用∠B、
BAC =2(90°-∠DEF-∠B),最后利用∠B、![]() BAC、
BAC、![]() C的和为180°求得三角之间的等量关系。
C的和为180°求得三角之间的等量关系。
试题解析:(1)∵EF⊥BC,∠DEF=10°,
∴∠EDF=80°.
∵∠B=40°,
∴∠BAD=∠EDF-∠B=80°-40°=40°.
∵AD平分∠BAC,∴∠BAC=80°.
∴∠C=180°-40°-80°=60°.
(2)∠C-∠B=2∠DEF.理由如下:
∵EF⊥BC,∴∠EDF=90°-∠DEF.
∵∠EDF=∠B+∠BAD,
∴∠BAD=90°-∠DEF-∠B.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=180°-2∠DEF-2∠B.
∴∠B+180°-2∠DEF-2∠B+∠C=180°.
∴∠C-∠B=2∠DEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抢微信红包成为节日期间人们最喜欢的活动之一,小明一家5个人抢到的红包数据如下:4,5,10,6,10.则这组数据的中位数和众数是( )
A.10,10B.7,8C.6,10D.8,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣mx+2m=0有两个相等的实数根,则m等于( )
A.0或8
B.0
C.8
D.2 -
科目: 来源: 题型:
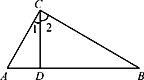
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是高.
(1)图中有几个直角三角形?是哪几个?
(2)∠1和∠A有什么关系?∠2和∠A呢?还有哪些锐角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x-2)2+1的顶点坐标是( )
A. (2,1) B. (-2,1) C. (2,-1) D. (-2,-1)
-
科目: 来源: 题型:
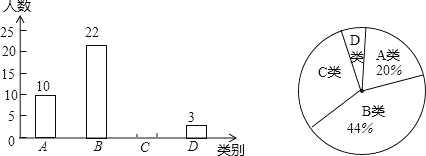
查看答案和解析>>【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试,并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)本次抽取样本容量为 ,扇形统计图中A类所对的圆心角是 度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-2,a)和点B(b,-5)关于x轴对称,则a+b=___________。
相关试题

