【题目】对于实数![]() ,
,![]() 定义两种新运算“※”和“
定义两种新运算“※”和“![]() ”:
”: ![]() ※
※![]() ,
,![]() (其中
(其中![]() 为常数,且
为常数,且![]() ,若对于平面直角坐标系
,若对于平面直角坐标系![]() 中的点
中的点![]() ,有点
,有点![]() 的坐标
的坐标![]() ※
※![]() ,
,![]() 与之对应,则称点
与之对应,则称点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() .例如:
.例如:![]() 的“2衍生点”为
的“2衍生点”为![]() ,即
,即![]() .
.
(1)点![]() 的“3衍生点”的坐标为 ;
的“3衍生点”的坐标为 ;
(2)若点![]() 的“5衍生点”
的“5衍生点” ![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 的“
的“![]() 衍生点”为点
衍生点”为点![]() ,且直线
,且直线![]() 平行于
平行于![]() 轴,线段
轴,线段![]() 的长度为线段
的长度为线段![]() 长度的3倍,求
长度的3倍,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)点
;(2)点![]() ;(3)k=±3.
;(3)k=±3.
【解析】
(1)直接利用新定义进而分析得出答案;
(2)直接利用新定义结合二元一次方程组的解法得出答案;
(3)先由![]() 轴得出点
轴得出点![]() 的坐标为
的坐标为![]() ,继而得出点
,继而得出点![]() 的坐标为
的坐标为![]() ,由线段
,由线段![]() 的长度为线段
的长度为线段![]() 长度的3倍列出方程,解之可得.
长度的3倍列出方程,解之可得.
(1)点![]() 的“3衍生点”
的“3衍生点” ![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
故答案为:![]() ;
;
(2)设![]()
依题意,得方程组![]() .
.
解得![]() .
.
![]() 点
点![]() ;
;
(3)设![]() ,则
,则![]() 的坐标为
的坐标为![]() .
.
![]() 平行于
平行于![]() 轴
轴
![]() ,即
,即![]() ,
,
又![]() ,
,
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 线段
线段![]() 的长度为
的长度为![]() .
.
![]() 线段
线段![]() 的长为
的长为![]() .
.
根据题意,有![]() ,
,
![]() .
.
∴k=±3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线
 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
(1)求S△ABD的值;
(2)如图2,若点P是直线AD下方抛物线上一动点,过点P作PF∥y轴交直线AD于点F,作PG∥AC交直线AD于点G,当△PGF的周长最大时,在线段DE上取一点Q,当PQ+
 QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+  QE的值;
QE的值;(3)如图3,M是BC的中点,以CM为斜边作直角△CMN,使CN∥x轴,MN∥y轴,将△CMN沿射线CB平移,记平移后的三角形为△C′M′N′,当点N′落在x轴上即停止运动,将此时的△C′M′N′绕点C′逆时针旋转(旋转度数不超过180°),旋转过程中直线M′N′与直线CA交于点S,与y轴交于点T,与x轴交于点W,请问△CST是否能为等腰三角形?若能,请求出所有符合条件的WN′的长度;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以已知线段
 为弦作⊙
为弦作⊙ ,使其经过已知点
,使其经过已知点 .
.(
 )利用直尺和圆规作圆(保留作图痕迹,不必写出作法).
)利用直尺和圆规作圆(保留作图痕迹,不必写出作法).(
 )若
)若 ,
,  ,求过
,求过 、
、 、
、 三点的圆的半径.
三点的圆的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学计划为学校科技活动小组购买
 型、
型、 型两种型号的放大镜.若购买8个
型两种型号的放大镜.若购买8个 型放大镜和5个
型放大镜和5个 型放大镜需用235元,购买4个
型放大镜需用235元,购买4个 型放大镜和6个
型放大镜和6个 型放大镜需用170元.
型放大镜需用170元.(1)求每个
 型放大镜和每个
型放大镜和每个 型故大镜各多少元?
型故大镜各多少元?(2)该中学决定购买
 型放大镜和
型放大镜和 型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个
型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个 型放大镜?
型放大镜? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
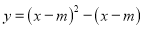 ,其中
,其中 是常数,该抛物线的对称轴为直线
是常数,该抛物线的对称轴为直线 .
.(
 )求该抛物线的函数解析式.
)求该抛物线的函数解析式.(
 )把该抛物线沿
)把该抛物线沿 轴向上平移多少个单位后,得到的抛物线与
轴向上平移多少个单位后,得到的抛物线与 轴只有一个公共点.
轴只有一个公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
相关试题

