【题目】如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:如图,延长GP交DC于点H,

∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴ ![]() =
= ![]() ;
;
所以答案是:B.
【考点精析】掌握菱形的性质和锐角三角函数的定义是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于点D,交AB于点E,CD=2,则AC等于( )
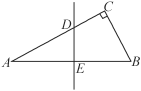
A. 4 B. 5 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:cos30°
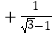 +|1﹣
+|1﹣ 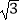 |﹣(
|﹣(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )
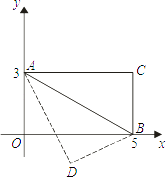
A.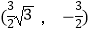
B.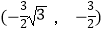
C.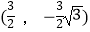
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把等边三角形ABD和等边三角形BCD拼合在一起,点E在AB边上移动,且满足AE=BF,试说明不论点E怎样移动,△EDF总是等边三角形.
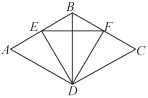
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,一天上午6点钟,言老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程s(km)(即离开学校的距离)与时间(时)的关系可用图中的折线表示,根据图中提供的有关信息,解答下列问题:
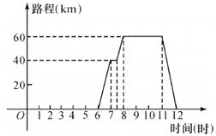
(1)开会地点离学校多远?
(2)请你用一段简短的话,对言老师从上午6点到中午12点的活动情况进行描述.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别从相距30千米的A、B两地同时相向而行,经过3小时后相距3千米,再经过2小时,甲到B地所剩的路程是乙到A地所剩路程的2倍,试求甲、乙两人的速度.
相关试题

