【题目】
(1)如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF
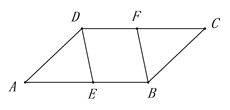
(2)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.

参考答案:
【答案】(1)证明见解析;(2)![]() =125°.
=125°.
【解析】试题分析:(1)本题利用三角形全等即可求出,或是证明四边形DEBF是平行四边形;(2)本题利用切线的性质得出∠BOD的度数,根据等边对等角,得出∠ADO的度数,即可求出∠CDA的度数.
试题解析:
证明:(方法一)
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF.
∴BE=FD,BE∥FD,
∴四边形EBFD是平行四边形,
∴DE=BF.
(方法二)
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,
又∵AE=CF, ∴![]() ,所以DE=BF.
,所以DE=BF.
(2)证明:连接![]() ,
,
∵CD与⊙O相切于点D,
∴OD⊥CD,∴∠ODC=90°
∵![]() =20°,∴∠COD=70°
=20°,∴∠COD=70°
∵OA=OD,∴∠ODA=35°
∴![]() =90°+35°=125°
=90°+35°=125°
-
科目: 来源: 题型:
查看答案和解析>>【题目】
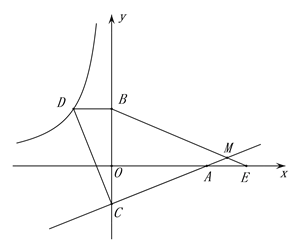
如图,已知点D在反比例函数y=
 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= .
.(1)求反比例函数y=
 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M,N表示单项式,且3x(M-5x)=6x2y3+N,则( )
A. M=2xy3,N=-15x B. M=3xy3,N=-15x2
C. M=2xy3,N=-15x2 D. M=2xy3,N=15x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是﹣1,且a、b、c满足(c﹣6)2+|2a+b|=0,请回答问题:
(1)请直接写出b、c的值:b= , c=
(2)在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x,
(a)当点P在AB间运动(不包括A、B),试求出P点与A、B、C三点的距离之和.
(b)当点P从A点出发,向右运动,请根据运动的不同情况,化简式子:|x+1|﹣|x﹣2|+2|x﹣6|(请写出化简过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】使(x2+px+8)(x2﹣3x+q)乘积中不含x2和x3项的p,q的值分别是( )
A.p=3,q=1
B.p=﹣3,q=﹣9
C.p=0,q=0
D.p=﹣3,q=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】小宇家新买的一套住房的建筑平面图如图所示(单位:米).
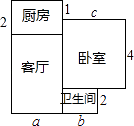
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=8,b=3,c=6,试求出小宇家这套住房的具体面积.
(3)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中:
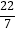 ,0,π,
,0,π, 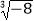 ,
, 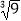 ,0.32,(
,0.32,( 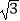 )0 ,
)0 , 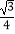 ,0.1010010001…中,无理数个数有( )
,0.1010010001…中,无理数个数有( )
A.3个
B.4个
C.5个
D.6个
相关试题

