【题目】
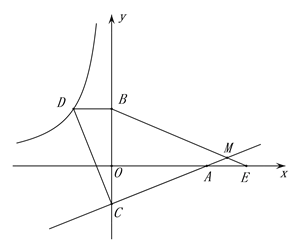
如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
参考答案:
【答案】(1)反比例函数的解析式为: ![]() 一次函数的解析式为:
一次函数的解析式为: ![]() ;
;
(2)![]() ,理由见解析;
,理由见解析;
(3)![]()
【解析】试题分析:(1)由点A(5,0)和tan∠OAC=![]() 可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出
可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出![]() ,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出
,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出![]() ,继而求出
,继而求出![]() .
.
试题解析:
(1)∵A(5,0),∴OA=5.
∵![]() ∴
∴![]()
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
设直线AC关系式为![]() ∵过A(5,0),
∵过A(5,0),![]()
∴![]() 解得:
解得: 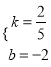 ∴
∴![]() .
.
(2)∵![]() ∴
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ∴
∴,
∴![]()
∴![]() .
.
(3) ![]()
连接AD,
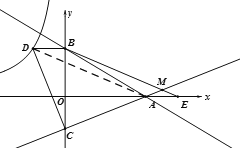
∵![]() ,
, ![]() ∴
∴![]()
∴四边形AEBD为平行四边形,∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∵![]() ∴
∴![]()
∴![]() =45°
=45°
-
科目: 来源: 题型:
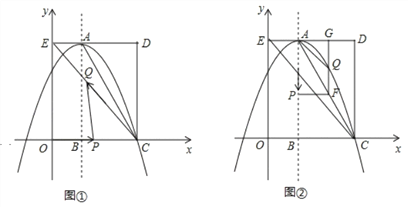
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. -a(a+1)=-a2+1 B. a(-a+1)=-a2-1
C. -x2(x-1)=x3+x2 D. (-x)2·(x-1)=x3-x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校九年级400名学生的体重,从中抽取了50名学生的体重进行统计分析,在这个问题中,总体是指( )
A. 400名学生B. 被抽取的50名学生
C. 400名学生的体重D. 被抽取的50名学生的体重
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M,N表示单项式,且3x(M-5x)=6x2y3+N,则( )
A. M=2xy3,N=-15x B. M=3xy3,N=-15x2
C. M=2xy3,N=-15x2 D. M=2xy3,N=15x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是﹣1,且a、b、c满足(c﹣6)2+|2a+b|=0,请回答问题:
(1)请直接写出b、c的值:b= , c=
(2)在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x,
(a)当点P在AB间运动(不包括A、B),试求出P点与A、B、C三点的距离之和.
(b)当点P从A点出发,向右运动,请根据运动的不同情况,化简式子:|x+1|﹣|x﹣2|+2|x﹣6|(请写出化简过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】
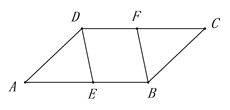
(1)如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF
(2)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.

相关试题

