【题目】如图,顶点为P(4,﹣4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,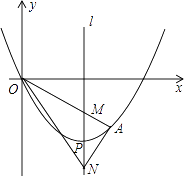
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,﹣3),求△ANO的面积;
(3)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
参考答案:
【答案】
(1)
解:∵二次函数的顶点坐标为(4,﹣4),
∴设二次函数的解析式为y=a(x﹣4)2﹣4,
又二次函数过(0,0),
∴0=a(0﹣4)2﹣4,解得:a= ![]() ,
,
∴二次函数解析式为y= ![]() (x﹣4)2﹣4=
(x﹣4)2﹣4= ![]() x2﹣2x
x2﹣2x
(2)
解:设直线OA的解析式为y=kx,将A(6,﹣3)代入得﹣3=6k,解得k=﹣ ![]() ,
,
∴直线OA的解析式为y=﹣ ![]() x,
x,
把x=4代入y=﹣ ![]() x得y=﹣2,
x得y=﹣2,
∴M(4,﹣2),
又∵点M、N关于点P对称,
∴N(4,﹣6),
∴MN=4,
∴S△ANO= ![]() ×6×4=12
×6×4=12
(3)
解:①证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:
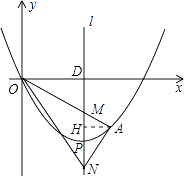
设A(m, ![]() m2﹣2m),又O(0,0),
m2﹣2m),又O(0,0),
∴直线AO的解析式为y= ![]() x=(
x=( ![]() m﹣2)x,
m﹣2)x,
则M(4,m﹣8),N(4,﹣m),H(4, ![]() m2﹣2m),
m2﹣2m),
∴OD=4,ND=m,HA=m﹣4,NH=ND﹣HD= ![]() m2﹣m,
m2﹣m,
在Rt△OND中,tan∠ONM= ![]() =
= ![]() ,
,
在Rt△ANH中,tan∠ANM= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠ONM=tan∠ANM,
则∠ANM=∠ONM;
②△ANO能为直角三角形,理由如下:
分三种情况考虑:
(i)若∠ONA为直角,由①得:∠ANM=∠ONM=45°,
∴△AHN为等腰直角三角形,
∴HA=NH,即m﹣4= ![]() m2﹣m,
m2﹣m,
整理得:m2﹣8m+16=0,即(m﹣4)2=0,
解得:m=4,
此时点A与点P重合,故不存在A点使△ONA为直角三角形;
(ii)若∠AON为直角,根据勾股定理得:OA2+ON2=AN2,
∵OA2=m2+( ![]() m2﹣2m)2,ON2=42+m2,AN2=(m﹣4)2+(
m2﹣2m)2,ON2=42+m2,AN2=(m﹣4)2+( ![]() m2﹣2m+m)2,
m2﹣2m+m)2,
∴m2+( ![]() m2﹣2m)2+42+m2=(m﹣4)2+(
m2﹣2m)2+42+m2=(m﹣4)2+( ![]() m2﹣2m+m)2,
m2﹣2m+m)2,
整理得:m(m2﹣8m﹣16)=0,
解得:m=0或m=4+4 ![]() 或4﹣4
或4﹣4 ![]() (舍去),
(舍去),
当m=0时,A点与原点重合,故∠AON不能为直角,
当m=4+4 ![]() ,即A(4+4
,即A(4+4 ![]() ,4)时,N为第四象限点,成立,故∠AON能为直角;
,4)时,N为第四象限点,成立,故∠AON能为直角;
(iii)若∠NAO为直角,可得∠NAM=∠ODM=90°,且∠AMN=∠DMO,
∴△AMN∽△DMO,
又∠MAN=∠ODN=90°,且∠ANM=∠OND,
∴△AMN∽△DON,
∴△AMN∽△DMO∽△DON,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得:(m﹣4)2=0,
解得:m=4,
此时A与P重合,故∠NAO不能为直角,
综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO能为直角三角形,当m=4+4 ![]() ,即A(4+4
,即A(4+4 ![]() ,4)时,N为第四象限点,成立,故∠AON能为直角
,4)时,N为第四象限点,成立,故∠AON能为直角
【解析】(1)由二次函数的顶点坐标,设出二次函数的顶点式,再由二次函数过原点,将原点坐标代入设出的解析式中,确定出a的值,即可求出二次函数的解析式;(2)首先通过求出OA直线方程求出M点的坐标,再通过对称性求出N点的坐标,进而求出MN的长度,△ANO的面积可以通过A点的横坐标长度和MN的长度计算得到;(3)①过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证;
②△ANO不能为直角三角形,理由为:分三种情况考虑:若∠ONA为直角,由①得到∠ANM=∠ONM=45°,可得出三角形AHN为等腰直角三角形,得到AH=HN,将表示出的AH及HN代入,得到关于m的方程,求出方程的解得到m的值为0或4± ![]() ,进而得到此时A与P重合,不合题意,故∠ONA不能为直角;若∠AON为直角,利用勾股定理得到OA2+ON2=AN2 , 由A的坐标,利用勾股定理表示出OA2 , 由OD及DN,利用勾股定理表示出ON2 , 由AH及HN,利用勾股定理表示出AN2 , 代入OA2+ON2=AN2 , 得到关于m的方程,求出方程的解得到m的值为4±4
,进而得到此时A与P重合,不合题意,故∠ONA不能为直角;若∠AON为直角,利用勾股定理得到OA2+ON2=AN2 , 由A的坐标,利用勾股定理表示出OA2 , 由OD及DN,利用勾股定理表示出ON2 , 由AH及HN,利用勾股定理表示出AN2 , 代入OA2+ON2=AN2 , 得到关于m的方程,求出方程的解得到m的值为4±4 ![]() 或0,然后判断∠AON是否为直角;若∠NAO为直角,则有△AMN∽△DMO∽△DON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NAO不能为直角,综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO不能为直角三角形.
或0,然后判断∠AON是否为直角;若∠NAO为直角,则有△AMN∽△DMO∽△DON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NAO不能为直角,综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO不能为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有学生2100人,在“文明我先行”活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了100名学生,并制成统计表:校本课程意向统计表
课程类型
频数
频率(%)
法律
s
0.08
礼仪
a
0.20
环保
27
0.27
感恩
b
m
互助
15
0.15
合计
100
1.00
请根据统计表的信息,解答下列问题;
(1)在这次调查活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);
(2)a= , b= , m=;
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程对应的扇形圆心角的度数是;
(4)请你估计,选择“感恩”类校本课程的学生约有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),结合所给的平面直角坐标系解答下列问题:
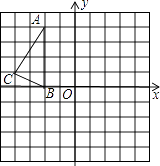
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移到点A2(0,2),画出平移后△A2B2C2并写出点B2、C2的坐标;
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与成中心对称,其对称中心坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在矩形ABCD中,把∠B、∠D分别翻折,使点B、D恰好落在对角线AC上的点E、F处,折痕分别为CM、AN,

(1)求证:△ADN≌△CBM;
(2)请连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图(2)所示,若PQ=CQ,PQ∥MN,且AB=4cm,BC=3cm,求PC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】第十六届亚远会共颁发金牌477枚,如图是不完整的金牌数条形统计图和扇形统计图,


根据以上信息.觯答下列问题:
(1)请将条形统计图补充完整;
(2)中国体育健儿在第十六届亚运会上共夺得金牌枚;
(3)在扇形统计图中,日本代表团所对应的扇形的圆心角约为°(精确到1°). -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中建立如图所示的平面直角坐标系xoy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1 , 并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.

(1)求证:△BDQ≌△ADP;
(2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号).
相关试题

