【题目】某校随机选取了![]() 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计该校学生同时喜欢短跑和跳绳的概率;
(2)估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
参考答案:
【答案】(1)同时喜欢短跑和跳绳的概率为![]() ;(2)同时喜欢三个项目的概率为
;(2)同时喜欢三个项目的概率为![]()
【解析】
(1)观察表格可知1000名学生中同时喜欢短跑和跳绳的学生有150名,根据概率公式即可求得该校学生同时喜欢短跑和跳绳的概率;(2)观察表格可知:1000名学生中,在长跑、短跑、跳绳、跳远中同时喜欢三个项目的学生有(200+150)名,根据概率公式即可求得该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率.
(1)同时喜欢短跑和跳绳的概率为:![]() ;
;
(2)同时喜欢三个项目的概率为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C.
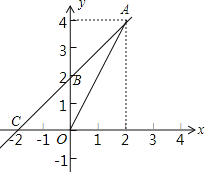
(1)写出点A、B、C的坐标;
(2)求此一次函数的解析式;
(3)求△AOC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量
 (万件)是销售单价
(万件)是销售单价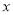 (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:销售单价
 (元)
(元)12
14
16
18
年销售量
 (万件)
(万件)7
6
5
4
(1)求出
 关于
关于 的函数关系式;
的函数关系式;(2)写出该公司销售这种产品的年利润
 (万元)关于销售单价
(万元)关于销售单价 (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价 为何值时,年利润最大?
为何值时,年利润最大?(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价
 的范围).
的范围). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】蔬菜店店主老王,近两天经营的白菜和西兰花的情况如下:
(1)昨天的白菜和西兰花的进价和售价如下表,老王用
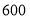 元,批发白菜和西兰花共
元,批发白菜和西兰花共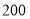 斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?
斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?白菜
西兰花
进价(元/斤)
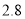
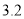
售价(元/斤)

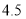
(2)今天因进价不变,老王仍用
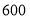 元批发白菜和西兰花共
元批发白菜和西兰花共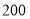 斤.但在运输中白菜损坏了
斤.但在运输中白菜损坏了 ,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到
,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到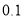 元)
元) -
科目: 来源: 题型:
查看答案和解析>>【题目】(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=
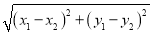 .
.例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=
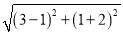 =
=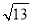 .
.【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
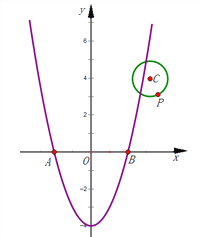
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 是线段
是线段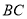 上一点,
上一点, ,
, .
.
(1)若
 是
是 的高线,且
的高线,且 ,求
,求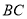 的长.
的长.
(2)若
 是
是 的角平分线,
的角平分线, ,求出
,求出 的面积.
的面积.
(3)填空:若
 是
是 的中线,设
的中线,设 长为
长为 ,则
,则 的取值范围______.
的取值范围______.
相关试题

