【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量![]() (万件)是销售单价
(万件)是销售单价![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价![]() 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价![]() 的范围).
的范围).
参考答案:
【答案】(1)y![]() ;(2)当x=18时,年利润最大;(3)
;(2)当x=18时,年利润最大;(3)![]() .
.
【解析】分析:(1)根据表中的已知点的坐标利用待定系数法确定一次函数的解析式即可;(2)根据总利润=单件利润×销量列出函数关系式,化为顶点式即可确定最值;
(3)令利润大于等于20,求得相应的自变量取值范围,即可解答本题.
本题解析:(1)设y=kx+b,
∵(16,5),(18,4)在此一次函数的图象上,
∴![]() ,
,
解得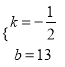 ,
,
故y关于x的函数关系式是:y=![]() x+13;
x+13;
故答案为:y=![]() x+13;
x+13;
(2)∵该公司年利润w=(![]() x+13)(x10)10=
x+13)(x10)10=![]() (x18)+22,
(x18)+22,
∴当x=18时,该公司年利润最大值为22万元,
即该公司销售这种产品的年利润w(万元)关于销售单价x(元)的函数关系式是:
w=![]() (x18)+22,当销售单价x为18时,年利润最大;
(x18)+22,当销售单价x为18时,年利润最大;
(3)年利润不低于20万元时x的取值范围是:16x20,
理由:∵![]() (x18)2+2220
(x18)2+2220
解得:16x20.
即年利润不低于20万元时x的取值范围是:16x20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
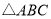 中,
中, ,
,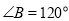 ,
,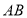 的垂直平分线交
的垂直平分线交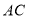 于点
于点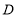 ,交
,交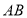 于点
于点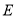 ,若
,若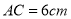 ,则
,则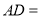 ________
________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C.
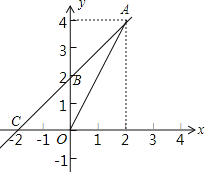
(1)写出点A、B、C的坐标;
(2)求此一次函数的解析式;
(3)求△AOC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机选取了
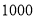 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.项目
学生数长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×
(1)估计该校学生同时喜欢短跑和跳绳的概率;
(2)估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
-
科目: 来源: 题型:
查看答案和解析>>【题目】蔬菜店店主老王,近两天经营的白菜和西兰花的情况如下:
(1)昨天的白菜和西兰花的进价和售价如下表,老王用
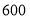 元,批发白菜和西兰花共
元,批发白菜和西兰花共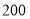 斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?
斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?白菜
西兰花
进价(元/斤)
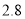
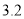
售价(元/斤)

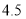
(2)今天因进价不变,老王仍用
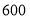 元批发白菜和西兰花共
元批发白菜和西兰花共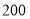 斤.但在运输中白菜损坏了
斤.但在运输中白菜损坏了 ,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到
,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到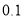 元)
元)
相关试题

