【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥AC交ED延长线于点F,则四边形BCEF周长的最小值为( )

A. 1+![]() B. 4 C. 2+
B. 4 C. 2+![]() D. 2+
D. 2+![]()
参考答案:
【答案】C
【解析】
由△ADE≌△BDF,推出BF=AE,推出四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,由题意易知BC=1,AC=![]() ,即可推出EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小.
,即可推出EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小.
∵BF∥AC,
∴∠A=∠FBD,
在△ADE和△BDF中,
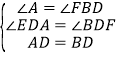 ,
,
∴△ADE≌△BDF,
∴BF=AE,
∴四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,
由题意易知BC=1,AC=![]() ,
,
∴EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小,
∵BD=AD,DE∥CB,
∴CE=AE,
∴DE=![]() BC=
BC=![]() ,
,
∴EF=2DE=1,
∴四边形BCEF周长的最小值为2+![]() .
.
故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).
(1)求三角形ABC的面积;
(2)如果三角形ABC的三个顶点的纵坐标不变,横坐标增加3个单位长度,得到三角形A1B1C1,试在图中画出三角形A1B1C1,并写出点A1,B1,C1的坐标;
(3)(2)中三角形A1B1C1与三角形ABC的大小、形状有什么关系?
-
科目: 来源: 题型:
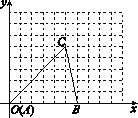
查看答案和解析>>【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4 cm,OA=5 cm,DE=2 cm,动点P从点A出发,以每秒1 cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2 cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,运动停止.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3 s时,求三角形PQC的面积;
(3)设两点运动的时间为t s,用含t的式子表示运动过程中三角形OPQ的面积.
-
科目: 来源: 题型:
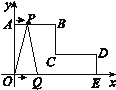
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )
A.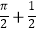
B.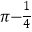
C.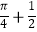
D.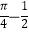
-
科目: 来源: 题型:
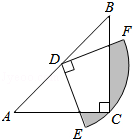
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BF与AD相交于E.若AD=BD,BE=AC,BC=8cm,DC=3cm,则AE=_____,∠BFC=_____.
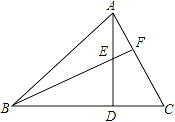
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,AC=DE,∠A=∠D.
(1)求证:AB=DF;
(2)若BC=9,EC=6,求BF的长.
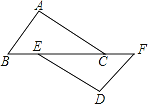
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)放入一个小球,量筒中水面升高_____________________________ cm;
(2)量筒中至少放入几个小球时有水溢出?
相关试题

