【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=3,AD=9,求△BDE的面积
参考答案:
【答案】
(1)解:解:△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,(两直线平行,内错角相等)
∴∠EBD=∠EDB,(等量代换)
∴BE=DE,(等角对等边)
即△BDE是等腰三角形
(2)解: 设DE=x,则BE=x,AE=9-x,
在Rt△ABE中,由勾股定理得:
AB2+AE2=BE2
即32+(9-x)2=x2
解得:x=5
∴BE=DE=5
解:所以S△BDE= ![]() DE×AB=
DE×AB= ![]() ×5×3=7.5
×5×3=7.5
【解析】(1)由折叠可知,∠CBD=∠EBD,再由AD∥BC,得到∠CBD=∠EDB,即可得到∠EBD=∠EDB,于是BE=DE,即可证明等腰三角形;(2)设DE=x,则BE=x,AE=9-x,在Rt△ABE中,由勾股定理得求出x的值,再根据三角形面积公式求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年为阻击新冠疫情,某社区要了解每一栋楼的居民年龄情况,以便有针对性进行防疫.一志愿者得到某栋楼60岁以上人的年龄(单位:岁)数据如下:62,63,75,79,68,85,82,69,70.获得这组数据的方法是( )
A.直接观察B.实验C.调查D.测量
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空:(2a+b)(_______)=4a2+4ab+b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+1与x+3成正比例,且当x=5时,y=3
(1)求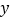 与
与 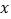 之间的函数关系式;、
之间的函数关系式;、
(2)当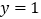 时,求
时,求 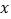 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区的电力资源丰富,并且得到了较好的开发。该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费. 月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
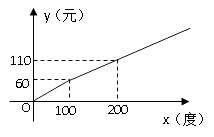
(1)月用电量为100度时,应交电费元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤6,请写出y与x的函数关系式.
(2)若x>6,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他。随机调查了该校
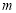 名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
名学生(每名学生必须且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图: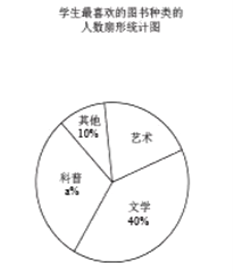
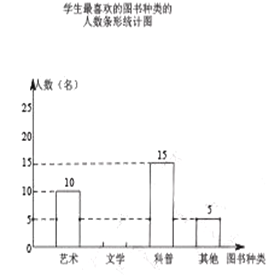
根据统计图提供的信息,解答下列问题:
(1)
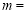 ,
,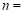 ;
;(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度.
(3)请根据以上信息直接在答题卡中补全条形统计图;
(4)根据抽样调查的结果,请你估计该校600名学生中有多少学生最喜欢科普类图书.
相关试题

