【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1 , ∠ABD1与∠ACD1的角平分线交于点D2 , 依此类推,∠ABD4与∠ACD4的角平分线交于点D5 , 则∠BD5C的度数是( ) 
A.24°
B.25°
C.30°
D.36°
参考答案:
【答案】B
【解析】∵∠A=20°,
∴∠ABC+∠ACB=180°-20°=160°,
∵∠ABC与∠ACB的角平分线交于D1 ,
∴∠D1BC+∠D1CB=80°,
由题意得,∴∠D2BC+∠D2CB=80°+40°=120°,
∴∠D3BC+∠D3CB=120°+20°=140°,
∴∠D4BC+∠D4CB=140°+10°=150°,
∴∠D5BC+∠D5CB=150°+5°=155°,
∴∠BD5C=180°-155°=25°.
根据∠A=20°,求出∠ABC+∠ACB的度数,根据题意依次求出∠D1BC+∠D1CB…∠D5BC+∠D5CB的度数,得到答案.本题考查的是三角形内角和定理和角平分线的定义,熟知三角形的内角和等于180°和角平分线的定义是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,点P在对角线BD上(不与点B , D重合),添加一个条件,使得△BCD与△ADP相似,这个条件可以是
-
科目: 来源: 题型:
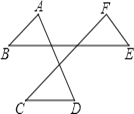
查看答案和解析>>【题目】如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180°
B.360°
C.540°
D.720° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点坐标为(﹣1,2),且经过点(0,4),求该函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
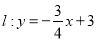 分别与x、y轴交于点A和B.
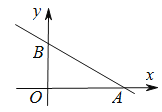
分别与x、y轴交于点A和B.(1)求点A、B的坐标;
(2)求原点O到直线的距离;
(3)若圆M的半径为2,圆心M在y轴上,当圆M与直线相切时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=-
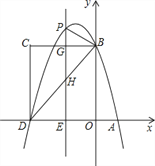
 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(-3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
相关试题

