【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
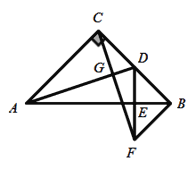
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△ACF是等腰三角形,理由见解析.
【解析】
(1)先由CG⊥AD得到∠AGC=90°,证得∠CAD=∠FCB,再由AC=BC,FB⊥BC,根据“ASA”即可得出结论;
(2)由(1)△ACD≌△CBF,得出CD=BF,证得BD=BF,由△ABC是等腰直角三角形,得出∠DBE=45°,再证得∠DBE=∠FBE=45°,由“SAS”证出△DBE≌△FBE即可得出结论;
(3)由△CBF≌△ACD,得出CF=AD,由AB垂直平分DF,得出AF=AD,证得CF=AF,即可得出结论.
证明:(1)∵CG⊥AD,
∴∠AGC=90°,
∴∠GCA+∠CAD=90°,
∵∠GCA+∠FCB=90°,
∴∠CAD=∠FCB,
∵FB⊥BC,
∴∠CBF=90°,
∵Rt△ABC是等腰三角形,∠ACB=90°,
∴AC=BC,∠CBF=∠ACB,
在△ACD和△CBF中
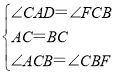 ,
,
∴△ACD≌△CBF(ASA);
(2)∵△ACD≌△CBF,
∴CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠DBE=45°,
∵∠CBF=90°,
∴∠DBE=∠FBE=45°,
在△DBE和△FBE中
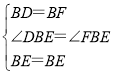 ,
,
∴△DBE≌△FBE(SAS),
∴DE=FE,∠DEB=∠FEB=90°,
∴AB垂直平分DF;
(3)△ACF是等腰三角形,理由为:
连接AF,如图所示,
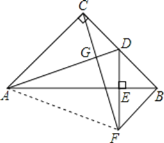
由(1)知:△CBF≌△ACD,
∴CF=AD,
由(2)知:AB垂直平分DF,
∴AF=AD,
∵CF=AD,
∴CF=AF,
∴△ACF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,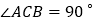 ,
, ,在
,在 上取一点
上取一点 ,在
,在 上取一点
上取一点 ,使
,使 ,过点
,过点 作
作 于点
于点 .交
.交 于点
于点 ,若
,若 ,
, ,则
,则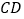 的长为________.
的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是菱形,
是菱形, 在
在 上,
上, 在
在 延长线上,
延长线上, 和
和 相交于点
相交于点 ,若
,若 ,
, ,
, 的长为
的长为 ,则菱形
,则菱形 的面积为________.
的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司举行周年庆典,决定订购一批印有公司logo的记事本赠送给客户,购买甲种记事本共花费3000元,购买乙种记事本共花费2100元,购买甲种记事本的数量是购买乙种记事本数量的2倍,且购买一个乙种记事本比购买一个甲种记事本多花20元.
(1)求购买一个甲种记事本,一个乙种记事本各需多少元?
(2)由于公司业务的扩大,公司决定再次购买甲、乙两种记事本共40个,且乙种记事本不少于23个,预算金额不超过2400元,购买时恰逢该店对两种记事本的售价进行调整,甲种记事本售价比第一次购买时提高了10%,乙种记事本售价比第一次购买时降低了10%,请问该公司有哪几种方案购买这批记事本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 如图
如图 ,
, 中,
中, 平分
平分 交
交 于点
于点 ,在
,在 上截取
上截取 ,过点
,过点 作
作 交
交 于点
于点 .求证:四边形
.求证:四边形 是菱形;
是菱形;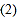 如图
如图 ,
, 中,
中, 平分
平分 的外角
的外角 交
交 的延长线于点
的延长线于点 ,在
,在 的延长线上截取
的延长线上截取 ,过点
,过点 作
作 交
交 的延长线于点
的延长线于点 .四边形
.四边形 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:(一)如果我们能找到两个实数x、y使
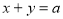 且
且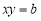 ,这样
,这样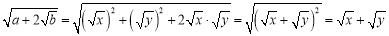 ,那么我们就称
,那么我们就称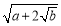 为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.例如:
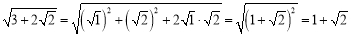 .
.(二)在进行二次根式的化简与运算时,我们有时还会碰上如
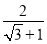 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: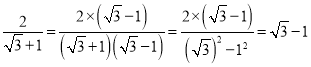 ,那么我们称这个过程为分式的分母有理化.
,那么我们称这个过程为分式的分母有理化.根据阅读材料解决下列问题:
(1)化简“和谐二次根式”:①
 ___________,②___________;
___________,②___________;(2)已知
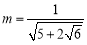 ,
,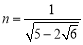 ,求
,求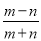 的值;
的值;(3)设
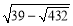 的小数部分为
的小数部分为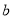 ,求证:
,求证: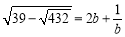 .
.
相关试题

