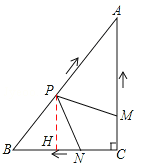
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
参考答案:
【答案】解:∵如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB=![]() 。
。
(1)以A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,![]() ,即
,即![]() ,解得
,解得![]() ;
;
②当△APM∽△ABC时,![]() ,即
,即![]() ,解得t=0(不合题意,舍去)。
,解得t=0(不合题意,舍去)。
综上所述,当![]() 时,以A、P、M为顶点的三角形与△ABC相似。
时,以A、P、M为顶点的三角形与△ABC相似。
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值。
如图,过点P作PH⊥BC于点H.则PH∥AC,
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∵![]() >0,∴S有最小值。
>0,∴S有最小值。
当t= ![]() 时,S最小值=
时,S最小值=![]() .
.
答:当t=![]() 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是![]() 。
。
【解析】
试题根据勾股定理求得AB=5cm。
(1)分△AMP∽△ABC和△APM∽△ABC两种情况讨论:利用相似三角形的对应边成比例来求t的值。
(2)如图,过点P作PH⊥BC于点H,构造平行线PH∥AC,由平行线分线段成比例求得以t表示的PH的值;然后根据“S=S△ABC﹣S△BPH”列出S与t的关系式![]() ,则由二次函数最值的求法即可得到S的最小值。
,则由二次函数最值的求法即可得到S的最小值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在
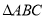 中,内角
中,内角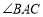 与外角
与外角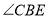 的平分线相交于点
的平分线相交于点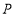 ,
,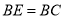 ,
,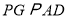 交
交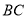 于
于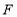 ,交
,交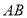 于
于 ,连接
,连接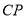 、
、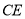 ,下列结论:①
,下列结论:①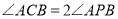 ;②
;② ;③
;③ 垂直平分
垂直平分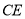 ;④
;④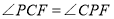 .其中正确的是( )
.其中正确的是( )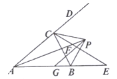
A. ①②④B. ①③④C. ②③④D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点,如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为_____________
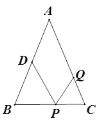
-
科目: 来源: 题型:
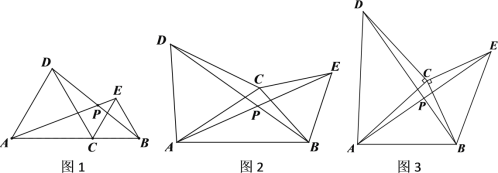
查看答案和解析>>【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

-
科目: 来源: 题型:
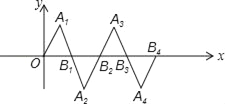
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
相关试题

