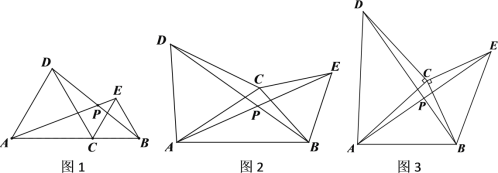
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
参考答案:
【答案】(1)AE=BD.∠APC=60°;(2)成立,见详解;(3)AE=BD
【解析】
(1)观察猜想:①证明△ACE≌△DCB(SAS),可得AE=BD,∠CAE=∠BDC;
②过点C向AE,BD作垂线,由三角形全等可得高相等,再根据角分线判定定理,推出PC平分∠APB,即可求出∠APC的度数;
(2)数学思考:结论成立,证明方法类似;
(3)拓展应用:证明△ACE≌△DCB(SAS),即可得AE=BD.
解:(1)观察猜想:结论:AE=BD.∠APC=60°.
理由: ①∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD;
②由①得∠EAC=∠BDC,
∵∠AOC=∠DOP,
∴∠APB=∠AOC+∠EAC=180°-60°= 120°.
过过点C向AE,BD作垂线交于点F与G
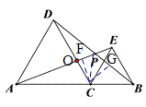
∵由①知△ACE≌△DCB
∴CF=CG
∴CP为∠APB的角平分线
∴∠APC=![]() 60°;
60°;
(2)数学思考:结论仍然成立.
①∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD;
②由①得∠AEC=∠DBC,
∴∠CEA+∠PEB=∠CBD+∠PEB=60°,
∴∠APB=∠CBD+∠CBE+∠PEB=120°.
过过点P向AC,BC作垂线交于点H与I
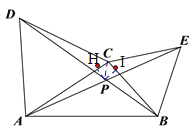
∵由①知△ACE≌△DCB
∴PH=PI
∴CP为∠APB的角平分线
∴∠APC=![]() 60°;
60°;
(3)∵△ADC,△ECB都是等腰直角三角形,
∴CA=CD,∠ACD=∠ECB=90°,CE=CB,
∴∠ACB+∠BCE=∠ACB+∠ACD
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=k1x+b与双曲线y=
 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点,如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为_____________
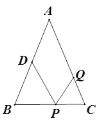
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

-
科目: 来源: 题型:
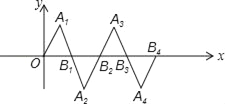
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金提高10元时,这种设备就少租一套,且未租出一套设备每月需要支出费用(维护费、管理费等)20元.
(1)设每套设备的月租金为
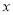 (元),用含
(元),用含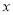 的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;(2)租赁公司的月收益能否达到11040元?此时应该出租多少套机械设备?每套月租金是多少元?请简要说明理由;
(3)租赁公司的月收益能否在11040元基础上再提高?为什么?
相关试题

