【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB. 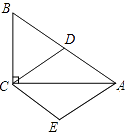
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
参考答案:
【答案】
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD= ![]() AB=BD=AD,
AB=BD=AD,
∴平行四边形ADCE是菱形
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CDsin60°=6× ![]() =3
=3 ![]() .
.
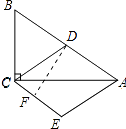
【解析】(1)先证明四边形ADCE是平行四边形,再证出一组邻边相等,即可得出结论;(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
(1)估计从袋中任意摸出一个球,恰好是红球的概率是多少?
(2)请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是
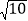 ,则“宝藏”点的坐标是( )
,则“宝藏”点的坐标是( )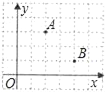
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
-
科目: 来源: 题型:
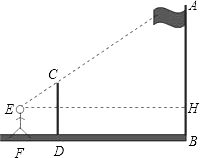
查看答案和解析>>【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
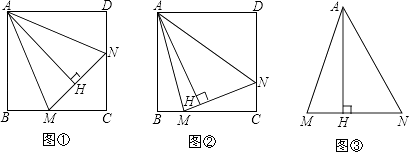
(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.(可利用(2)得到的结论) -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的
 ,
,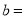 ;
;(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在
 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人?
相关试题

