【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=![]() (x>0)相交于点P(1,m).
(x>0)相交于点P(1,m).
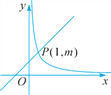
(1)求k的值.
(2)若点Q与点P关于直线y=x对称,求点Q的坐标.
(3)若过P,Q两点的抛物线与y轴的交点为N(0, ![]() )求该抛物线的函数表达式及其对称轴.
)求该抛物线的函数表达式及其对称轴.
参考答案:
【答案】(1) k=1.(2) 点Q(2,1). (3) 解析式:y=-![]() x2+x+
x2+x+![]() ,对称轴:x=-
,对称轴:x=-![]()
【解析】分析:(1)直接利用图象上点的坐标性质进而代入求出即可;(2)连接PO,QO,PQ,作PA⊥y轴于A,QB⊥x轴于B,于是得到PA=1,OA=2,根据点Q与点P关于直线y=x成轴对称,得到直线y=x垂直平分PQ,根据线段垂直平分线的性质得到OP=OQ,根据全等三角形的性质得到QB=PA=1,OB=OA=2,于是得到结论;(3)设抛物线的函数解析式为y=ax+bx+c,把P、Q、N(0, ![]() )代入y=ax+bx+c,解方程组即可得到结论.
)代入y=ax+bx+c,解方程组即可得到结论.
本题解析:
(1)把点P(1,m)代入y=![]() ,得m=2,
,得m=2,
∴点P(1,2).
把点P(1,2)代入y=kx+1,得k=1.
(2)设点Q(a,b).
∵点Q与点P关于直线y=x对称,点P(1,2),
∴![]() =
=![]() ,∴b=a-1.
,∴b=a-1.
∵直线y=x过原点,
∴OP=OQ,∴![]() ,
,
解得a1=2,a2=-1(不合题意,舍去).∴点Q(2,1).
(3)设抛物线的函数表达式为y=ax2+bx+c.
由题意,得 解得
解得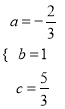
∴y=-![]() x2+x+
x2+x+![]() ,
,
∴对称轴为直线x=-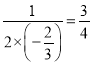 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.
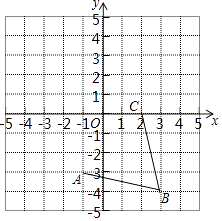
(1)请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标;
(2)菱形ABCD的周长为;
(3)菱形ABCD的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】y=x2+2的对称轴是直线( )
A.x=2
B.x=0
C.y=0
D.y=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3cm,圆心O到直线l的距离是2m,则直线l与⊙O的位置关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果盈利50元记作+50元,那么亏本30元记作:( )
A.﹣30元B.﹣50元C.+50元D.+30元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的边数增加1,它的内角和是2160°,那么原多边形的边数是( )
A.12B.13C.14D.15
相关试题

