【题目】已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH= . 
参考答案:
【答案】![]()
【解析】解:连结GE.

∵E是边AD的中点,
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°,
∴∠D=∠EFG=90°.
在Rt△EFG与Rt△EDG中,
![]() ,
,
∴Rt△EFG≌Rt△EDG(HL);
∴DG=FG=16,
设DC=x,则CG=16﹣x,BG=x+16
在Rt△BCG中,
BG2=BC2+CG2,
即(x+16)2=(16﹣x)2+242,
解得x=9,
∵AD∥BC,
∴∠AEB=∠CBE,
∵∠AEB=∠FEB,
∴∠CBE=∠FEB,
∴BH=EH,
设BH=EH=y,则FH=12﹣y,
在Rt△BFH中,
BH2=BF2+FH2,
即y2=92+(12﹣y)2,
解得y= ![]() ,
,
∴12﹣y=12﹣ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
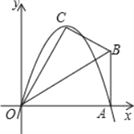
查看答案和解析>>【题目】已知在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作y轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运城市出租车价格是这样规定的:不超过3千米付车费5元;超过的部分按每千米1.6元收费,已知小颖乘出租车行驶了x(x>3)千米,付车费y元,则所付车费y元与出租车行驶的路程x千米之间的关系式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB,P是任一点,过点P画一条直线与OA平行,则这样的直线( )
A.有且仅有一条
B.有两条
C.不存在
D.有一条或不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.
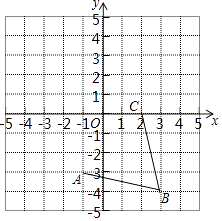
(1)请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标;
(2)菱形ABCD的周长为;
(3)菱形ABCD的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】y=x2+2的对称轴是直线( )
A.x=2
B.x=0
C.y=0
D.y=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y=
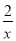 (x>0)相交于点P(1,m).
(x>0)相交于点P(1,m).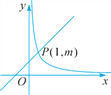
(1)求k的值.
(2)若点Q与点P关于直线y=x对称,求点Q的坐标.
(3)若过P,Q两点的抛物线与y轴的交点为N(0,
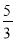 )求该抛物线的函数表达式及其对称轴.
)求该抛物线的函数表达式及其对称轴.
相关试题

