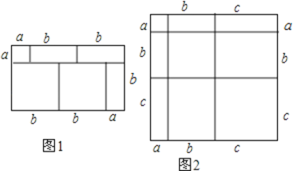
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用3张边长为a的正方形,4张边长为b的正方形,7张边长分别为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(5a+7b)(4a+9b)长方形,那么x+y+z= .
参考答案:
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)45;(3)3a+4b ;(4)156
【解析】
(1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;
(2)将a+b+c=11,ab+bc+ac=38代入(1)中得到的关系式,然后进行计算即可;
(3)先列出长方形的面积的代数式,然后分解代数式,可得到矩形的两边长;
(4)长方形的面积xa2+yb2+zab=(5a+7b)(4a+9b),然后运算多项式乘多项式法则求得(5a+7b)(4a+9b)的结果,从而得到x、y、z的值.
解:(1)正方形的面积可表示为=(a+b+c)2;
正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ca,
所以(a+b+c)2=a2+b2+c2+2ab+2bc+2ca.
(2)a2+b2+c2=(a+b+c)2-2ab-2ac-2bc,
=112-2×38,
=45;
(3)长方形的面积=3a2+7ab+4b2=(3a+4b)(a+b).
所以长方形的边长为3a+4b和a+b,
所以较长的一边长为3a+4b;
(4)∵长方形的面积=xa2+yb2+zab=(5a+7b)(4a+9b)
= 20a2+63b2+73ab,
∴x=20,y=63,z=73.
∴x+y+z=20+63+73=156.
故答案为:156.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
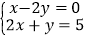 (2)
(2)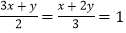
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2﹣4ac>0中错误的个数为( )
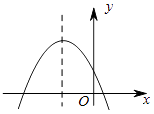
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】5.1劳动节,某校决定组织甲乙两队参加义务劳动,并购买队服.下面是服装厂给出的服装的价格表:
购买服装的套数
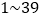 套
套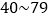 套
套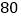 套以上
套以上每套服装的价格
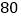 元
元 元
元 元
元经调查:两个队共75人(甲队人数不少于40人),如果分别各自购买队服,两队共需花费5600元,请回答以下问题:
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省_________.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人),现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请写出所有的抽调方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.

相关试题

