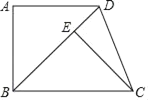
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,过点C作CE⊥BD交BD于点E,且CE=AB.
(1)求证:△ABD≌△ECB;
(2)若AB=AD,求∠ADC的度数.
参考答案:
【答案】(1)见解析;(2)∠ADC=112.5°
【解析】
(1)由“AAS”可证△ABD≌△ECB;
(2)由全等三角形的性质可得∠DBC=∠ADB=45°,BC=BD,由等腰三角形的性质可得∠BDC=67.5°,即可求∠ADC的度数.
(1)∵AD∥BC,
∴∠ADB=∠DBC.
∵∠A=∠BEC=90°,AB=CE,
∴△ABD≌△ECB(AAS);
(2)∵AB=AD,∠BAD=90°,
∴∠ADB=∠ABD=45°.
∵△ABD≌△ECB,
∴∠DBC=∠ADB=45°,BC=BD,
∴∠BDC=67.5°,
∴∠ADC=112.5°
-
科目: 来源: 题型:
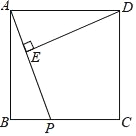
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)试说明△ADE∽△PAB;
(2)若PA=x,DE=y,请写出y与x之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
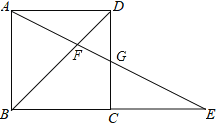
A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(4,2),BO=4
 ,反比例函数y=
,反比例函数y= 的图象经过点B,则k的值为_____.
的图象经过点B,则k的值为_____.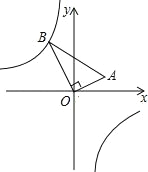
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
16
戏剧
4
散文
a
其他
b
合计
1
根据图表提供的信息,解答下列问题:
(1)直接写出a,b,m的值;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=
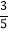 ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.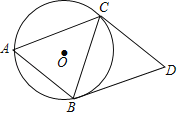
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

相关试题

