【题目】如图是一次函数![]() 的图像.
的图像.
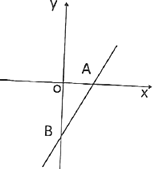
(1)设它的图像与![]() 轴
轴![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求
两点,求![]() 的长;
的长;
(2)求![]() 的面积;
的面积;
(3)求点![]() 到直线
到直线![]() 的距离.
的距离.
参考答案:
【答案】(1)AB=5;(2)S△AOB=6;(3)点O到直线AB的距离为![]() .
.
【解析】
(1)令x=0,代入一次函数解析式可求出y值,可得点B坐标;令y=0,代入一次函数解析式可求出x值,可得点A坐标,即可得出OA、OB的长,利用勾股定理求出AB的长即可;
(2)根据三角形面积公式即可得答案;
(3)过点O作OC⊥AB于C,则OC为点O到直线AB的距离,根据△AOB的面积即可求出OC的长,可得答案.
(1)∵一次函数的解析式为![]() ,
,
∴当x=0时,y=-4,当y=0时,x=3,
∴OA=3,OB=4,
∴AB=![]() =5.
=5.
(2)∵OA=3,OB=4,
∴△AOB的面积=![]() OA·OB=
OA·OB=![]() ×3×4=6.
×3×4=6.
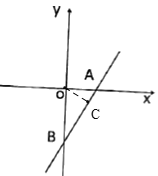
(3)如图,过点O作OC⊥AB于C,则OC为点O到直线AB的距离,
∵S△AOB=6,
∴![]() AB·OC=6,
AB·OC=6,
∵AB=5,
∴OC=![]() ,
,
∴点O到直线AB的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(﹣2,3)是反比例函数y=
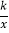 图象上的一点,则下列各点中,也在该函数图象上的是( )
图象上的一点,则下列各点中,也在该函数图象上的是( )A. (2,﹣3) B. (3,2) C. (﹣2,﹣3) D. (2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( ).

A. 3﹣
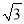 B. 2
B. 2 ﹣3 C. 2
﹣3 C. 2 D. 3+
D. 3+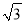
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )

A.①② B.①④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=
 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
相关试题

