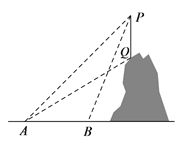
【题目】如图所示,某教学活动小组选定测量小山上方某信号塔PQ的高度,他们在A处测得信号塔顶端P的仰角为45°,信号塔低端Q的仰角为31°,沿水平地面向前走100米到处,测得信号塔顶端P的仰角为68°.求信号塔PQ的高度.(结果精确到0.1米.参考数据:sin68°≈ 0.93,cos68° ≈ 0.37,tan68° ≈ 2.48,tan31° ≈ 0.60,sin31° ≈ 0.52,cos31°≈0.86)
参考答案:
【答案】信号塔PQ的高度约为67.0米
【解析】延长PQ交直线AB于点E,连接AQ,设PM的长为x米,先由三角函数得出方程求出PM,再由三角函数求出QM,得出PQ的长度即可.
解:延长PQ交直线AB于点M,
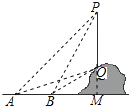
则∠PMA=90°,设PM的长为x米,根据题意,
得∠PAM=45°,∠PBM=68°,∠QAM=31°,
AB=100,∴在Rt△PAM中,AM=PM=x.
BM=AM-AB=x-100,
在Rt△PBM中,∵tan∠PBM=![]() ,
,
即tan68°=![]() .
.
解得x ≈ 167.57.∴AM=PM ≈ 167.57.
在Rt△QAM中,∵tan∠QAM=![]() ,
,
∴QM=AM·tan∠QAM=167.57×tan31°≈100.54.
∴PQ=PM-QM=167.57-100.54≈67.0(米).
因此,信号塔PQ的高度约为67.0米.
“点睛”本题考查直角三角形的应用、三角函数;由三角函数得出方程是解决问题的关键,注意掌握当两个直角三角形有公共边时,先求出这条公共边的边长是解答此类题的一般思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=(x﹣2)2+3的图象向右平移2个单位,再向下平移2个单位,所得二次函数的解析式为__.
-
科目: 来源: 题型:
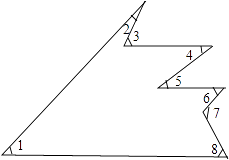
查看答案和解析>>【题目】如图,∠1=m°,∠2+∠4+∠6+∠8=n°,则∠3+∠5+∠7的大小是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:已知在△ABC中,边AB上的动点D由A向B运动(与A,B不重合),同时点E由点C沿BC的延长线方向运动(E不与C重合),连接DE交AC于点F,点H是线段AF上一点,求
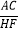 的值.
的值.(1)初步尝试
如图(1),若△ABC是等边三角形,DH⊥AC,且点D、E的运动速度相等,小王同学发现可以过点D作DG∥BC交AC于点G,先证GH=AH,再证GF=CF,
从而求得
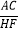 的值为 .
的值为 .(2)类比探究
如图(2),若△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是
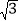 ︰1,求
︰1,求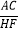 的值.
的值.(3)延伸拓展
如图(3)若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记
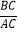 =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示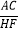 的值(直接写出果,不必写解答过程).
的值(直接写出果,不必写解答过程).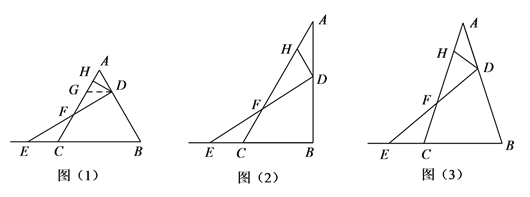
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一个数a的3倍与2的和”用代数式可表示为( )
A.3(a+2)
B.(3+a)a
C.2a+3
D.3a+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程2x+m-3(m-1)=1+x的解为负数,则m的范围是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2(x﹣3)2﹣4的最小值为 .
相关试题

