【题目】如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=![]() .
.
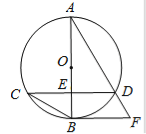
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长.
参考答案:
【答案】(1)见解析(2)2(3)![]()
【解析】解:(1)∵BF是⊙O的切线 ∴AB⊥BF …………………1分
∵AB⊥CD
∴CD∥BF………………………………………………2分
(2)连结BD
∵AB是直径 ∴∠ADB=90° ………………………………………3分
∵∠BCD=∠BAD cos∠BCD=![]() …………………4分
…………………4分
∴cos∠BAD=![]()
又∵AD=3 ∴AB=4
∴⊙O的半径为2 ……………………………………5分
(3)∵cos∠DAE=![]() AD=3∴AE=
AD=3∴AE=![]() …………………………6分
…………………………6分
∴ED= ……………………………………………7分
……………………………………………7分
∴CD=2ED=![]() ………………………………………………………8分
………………………………………………………8分
(1)由平行公理可得
(2)连结BD,利用三角函数求得![]() 通过已知,即可求得⊙O的半径
通过已知,即可求得⊙O的半径
(3)利用三角函数求得AE的长,通过勾股定理求得ED的长,从而求得弦CD的长
-
科目: 来源: 题型:
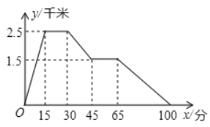
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在下列条件下,不是直角三角形的是( )
A.
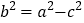 B.
B. 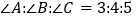
C.
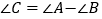 D.
D. 
-
科目: 来源: 题型:
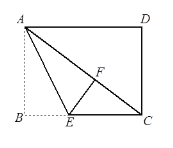
查看答案和解析>>【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.
(1)如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) 已知3×9m×27m=321,求m的值.
(2)(
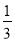 )﹣2+(2019﹣π)0÷(﹣2)﹣2﹣32;
)﹣2+(2019﹣π)0÷(﹣2)﹣2﹣32;(3)已知:
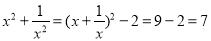 ,求 ①
,求 ①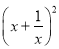 ,②
,② ,③
,③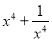 的值
的值
相关试题

