Question

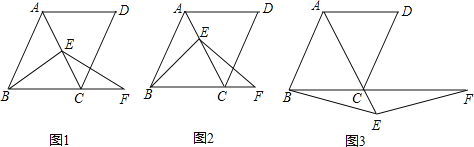
【题目】在菱形ABCD中，∠ABC=60°，E是对角线AC上一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF。

（1）若E是线段AC的中点，如图1，易证：BE=EF(不需证明)；

（2）若E是线段AC或AC延长线上的任意一点，其它条件不变， 如图2、图3，线段BE、EF有怎样的数量关系，直接写出你的猜想；并选择一种情况给予证明。

Answer 1

【答案】（2）BE=EF，证明见解析

【解析】解：（2）图2：BE=EF。图3。

图2证明如下：过点E作EG∥BC，交AB于点G，

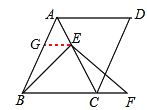
∵四边形ABCD为菱形，∴AB=BC。

又∵∠ABC=60°，∴△ABC是等边三角形。

∴AB=AC，∠ACB=60°。

又∵EG∥BC，∴∠AGE=∠ABC=60°。

又∵∠BAC=60°，∴△AGE是等边三角形。∴AG=AE。∴BG=CE。

又∵CF=AE，∴GE=CF。

又∵∠BGE=∠ECF=120°，∴△BGE≌△ECF（SAS）。∴BE=EF。

（1）根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形，再根据等腰三角形三线合一的性质可得∠CBE=∠ABC=30°，AE=CE，所以CE=CF，然后等边对等角的性质可得∠F=∠CEF，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°，从而得到∠CBE=∠F，根据等角对等边的性质即可证明。

（2）图2，过点E作EG∥BC，交AB于点G，

根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形，根据等边三角形的性质得到AB=AC，∠ACB=60°，再求出△AGE是等边三角形，根据等边三角形的性质得到AG=AE，从而可以求出BG=CE，再根据等角的补角相等求出∠BGE=∠ECF=120°，然后利用“边角边”证明△BGE和△ECF 全等，根据全等三角形对应边相等即可得证。

图3，证明思路与方法与图2完全相同， 证明如下：

过点E作EG∥BC交AB延长线于点G，

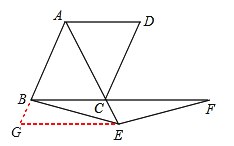
∵四边形ABCD为菱形，∴AB=BC。

又∵∠ABC=60°，∴△ABC是等边三角形。

∴AB=AC∠ACB=60°。

又∵EG∥BC，∴∠AGE=∠ABC=60°。

又∵∠BAC=60°，∴△AGE是等边三角形。∴AG=AE。∴BG=CE。

又∵CF=AE，∴GE=CF。

又∵∠BGE=∠ECF=60°，∴△BGE≌△ECF（SAS）。∴BE=EF。