【题目】等腰三角形一腰长为5,一边上的高为3,则底边长为 .
参考答案:
【答案】8或10或3![]()
【解析】如图所示:

当等腰三角形为锐角三角形,且CD为腰上的高时,
在Rt△ACD中,AC=5,CD=3,
根据勾股定理得:AD=![]() =4;
=4;
∴BD=AB-AD=5-4=1,
在Rt△BDC中,CD=3,BD=1,
根据勾股定理得:BC=![]() =
=![]() ;
;
当等腰三角形为钝角三角形,且CD为腰上的高时,
在Rt△ACD中,AC=5,CD=3,
根据勾股定理得:AD=![]() =4,
=4,
∴BD=AB+AD=5+4=9,
在Rt△BDC中,CD=3,BD=9,
根据勾股定理得:BC=![]() =3
=3![]() ;
;
当AD为底边上的高时,如图所示:
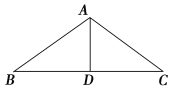
∵AB=AC,AD⊥BC,
∴BD=CD,
在Rt△ABD中,AD=3,AB=5,
根据勾股定理得:BD=![]() =4,
=4,
∴BC=2BD=8,综上,等腰三角形的底边长为8或![]() 或3
或3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若长方形面积是2a2﹣2ab+6a,一边长为2a,则这个长方形的周长是( )
A. 6a﹣2b+6B. 2a﹣2b+6C. 6a﹣2bD. 3a﹣b+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E、F分别是AB、BC边的中点,连接AF、CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE=
 :3;⑤S△EPM=
:3;⑤S△EPM=  S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
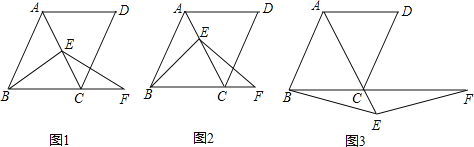
查看答案和解析>>【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF。
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变, 如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC向右平移3个单位长度再向下平移2个单位长度,画出两次平移后的△A1B1C1;
(2)写出A1、C1的坐标;
(3)将△A1B1C1绕C1逆时针旋转90°,画出旋转后的△A2B2C1,求线段B1C1旋转过程中扫过的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按
 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0)。
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且
 ,求点B的坐标。
,求点B的坐标。
相关试题

