【题目】数据3,2,4,2,5,3,2的中位数和众数分别是( )
A.2,3
B.4,2
C.3,2
D.2,2
参考答案:
【答案】C
【解析】解:把这组数据从小到大排列:2,2,2,3,3,4,5,
最中间的数是3,
则这组数据的中位数是3;
2出现了3次,出现的次数最多,则众数是2.
故选:C.
【考点精析】解答此题的关键在于理解中位数、众数的相关知识,掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个比﹣1小的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法将3.8963(精确到0.01)≈ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强用8块棱长为3 cm的小正方体,搭建了一个如图所示的积木,下列说法中不正确的是( )

A. 从左面看这个积木时,看到的图形面积是27cm2
B. 从正面看这个积木时,看到的图形面积是54cm2
C. 从上面看这个积木时,看到的图形面积是45cm2
D. 分别从正面、左面、上面看这个积木时,看到的图形面积都是72cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系;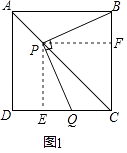
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.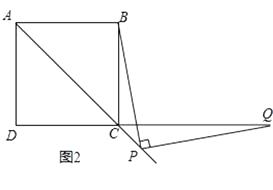
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分) 求一个正数的算术平方根,有些数可以直接求得,如
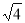 ,有些数则不能直接求得,如
,有些数则不能直接求得,如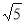 ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:n
16
0.16
0.0016
1600
160000
…
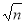
4
0.4
0.04
40
400
…
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知
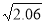
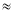 1.435,求下列各数的算术平方根:
1.435,求下列各数的算术平方根:①0.0206
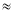 ; ②20600
; ②20600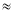 ;
; (3)根据上述探究过程类比研究一个数的立方根已知
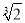
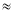 1.260,则
1.260,则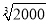
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

相关试题

