【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为 . 
参考答案:
【答案】2
【解析】解:过P作PE⊥OB,交OB与点E,

∵∠AOP=∠BOP,PD⊥OA,PE⊥OB,
∴PD=PE,
∵PC∥OA,
∴∠CPO=∠POD,
又∠AOP=∠BOP=15°,
∴∠CPO=∠BOP=15°,
又∠ECP为△OCP的外角,
∴∠ECP=∠COP+∠CPO=30°,
在直角三角形CEP中,∠ECP=30°,PC=4,
∴PE= ![]() PC=2,
PC=2,
则PD=PE=2.
故答案为:2.
过P作PE垂直与OB,由∠AOP=∠BOP,PD垂直于OA,利用角平分线定理得到PE=PD,由PC与OA平行,根据两直线平行得到一对内错角相等,又OP为角平分线得到一对角相等,等量代换可得∠COP=∠CPO,又∠ECP为三角形COP的外角,利用三角形外角的性质求出∠ECP=30°,在直角三角形ECP中,由30°角所对的直角边等于斜边的一半,由斜边PC的长求出PE的长,即为PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(x+3)(x﹣2)﹣(x﹣4)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解x3﹣4x的结果是( )
A.x(x2﹣4)
B.x(x﹣4)2
C.x(x﹣2)(x+2)
D.x(x﹣2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式8a3﹣8a2+2a的结果是( )
A.2a(2a﹣1)2
B.a(4a﹣1)2
C.a(2a﹣1)2
D.2a(2a+1)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示)
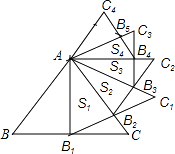
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,AF=EC,求证:四边形EBFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
(1)5(x+2)≥1-2(x-1);(2)
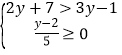 ;(3)
;(3) ;(4)
;(4)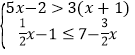
相关试题

