【题目】在△ABC中AB=AC，中线BD将△ABC的周长分为12cm和15cm，则三角形底边长_____．

参考答案：

【答案】11cm或7cm

【解析】试题解析：如图，∵AB=AC，BD是AC边上的中线，

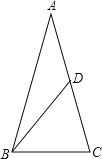
即AD=CD，

∴|(AB+AD)(BC+CD)|=|ABBC|=1512=3(cm)，AB+BC+AC=2AB+BC=12+15=27cm，

若AB>BC，则ABBC=3cm，

又∵2AB+BC=27cm，

联立方程组并求解得：AB=10cm，BC=7cm，

10cm、10cm、7cm三边能够组成三角形；

若AB<BC，则BCAB=3cm，

又2AB+BC=27cm，

联立方程组并求解得：AB=8cm，BC=11cm，

8cm、8cm、11cm三边能够组成三角形；

∴三角形的各边长为10cm、10cm、7cm或8cm、8cm、11cm.

故答案为：7cm或11cm.

关闭