搜索
【题目】点A在数轴上位于原点的左侧,距离原点3个单位长度,若将点A向右移动4个单位长度,再向左移动2个单位长度,此时点A表示的数是___.
参考答案：
【答案】-1
【解析】
根据题意先确定A点表示的数，再根据点在数轴上移动的规律，得出答案．
因为点A在数轴上距原点3个单位长度，且位于原点左侧，所以，点A表示的数为-3，将A向右移动4个单位长度，移动后点A所表示的数是：-3+4=1，然后向左移动2个单位长度，点A所表示的数为：1-2=-1．
故答案为：-1.
-
科目： 来源： 题型：
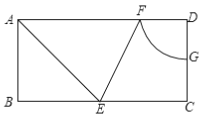
查看答案和解析>>【题目】如图，矩形ABCD中，BC=2AB=4，AE平分∠BAD交边BC于点E，∠AEC的分线交AD于点F，以点D为圆心，DF为半径画圆弧交边CD于点G，求FG的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠BDF=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（ ）
A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大，后由大到小
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读下面材料：
点A，B在数轴上分别表示实数a，b，A，B两点之间的距离表示为|AB|．
当A，B两点中有一点在原点时，不妨设点A在原点，如图（1），|AB|=|OB|=|b|=|a﹣b|；当A，B两点都不在原点时，
①如图（2），点A，B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；
②如图（3），点A，B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；
③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（﹣b）=|a﹣b|；
综上，数轴上A，B两点之间的距离|AB|=|a﹣b|．
（2）回答下列问题：
①数轴上表示2和5的两点之间的距离是 ，数轴上表示﹣2和﹣5的两点之间的距离是 ，数轴上表示1和﹣3的两点之间的距离是 ；
②数轴上表示x和﹣1的两点A和B之间的距离是 ，如果|AB|=2，那么x为 ；
③当代数式|x+1|+|x﹣2|取最小值时，相应的x的取值范围是 ．
④解方程|x+1|+|x﹣2|=5．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
（1）△BEF是等腰三角形吗？试说明理由；
（2）若AB＝4，AD＝8，求CF的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位，体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中，∠ACB=90°，若
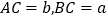，请你利用这个图形解决下列问题：（1）试说明
；（2）如果大正方形的面积是10，小正方形的面积是2，求
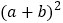的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求，欲购进一批学生喜欢的图书.学校组织学生会成随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类.根据调查结果绘制了统计图（未完成）.请根据图中信息，解答下列问题：
（1）此次共调查了 名学生；
（2）将条形统计图补充完整；
（3）图2中“小说类”所在扇形的圆心角为 度；
（4）若该学校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数.
相关试题
