【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

参考答案:
【答案】①3,3,4②|x+1|,1或-3③-1≤x≤2④x=3或x=-2
【解析】试题分析:①②直接根据数轴上A、B两点之间的距离|AB|=|a﹣b|.代入数值运用绝对值即可求任意两点间的距离.
③根据绝对值的性质,可得到一个一元一次不等式组,通过求解,就可得出x的取值范围.
④根据题意分三种情况:当x≤﹣1时,当﹣1<x≤2时,当x>2时,分别求出方程的解即可.
试题解析:①数轴上表示2和5的两点之间的距离是|2﹣5|=3;
数轴上表示﹣2和﹣5的两点之间的距离是|﹣2﹣(﹣5)|=3;
数轴上表示1和﹣3的两点之间的距离是|1﹣(﹣3)|=4
②数轴上x与-1的两点间的距离为|x-(-1)|=|x+1|,如果|AB|=2,则x+1=±2,解得x=1或
-3.
③根据题意得x+1≥0且x-2≤0,则-1≤x≤2;
④解方程|x+1|+|x﹣2|=5.
当x+1>0,x-2>0,则(x+1)+(x-2)=5,解得x=3
当x+1<0,x-2<0,则-(x+1)-(x-2)=5,解得x=-2
当x+1与x-2异号,则等式不成立.
所以答案为:3或-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B的坐标分别为A(-4,0)、B(2,0),点C在y轴上,且△ABC的面积为6,以点A、B、C为顶点作□ABCD.若过原点的直线平分该□ABCD的面积,则此直线的解析式是________.
-
科目: 来源: 题型:
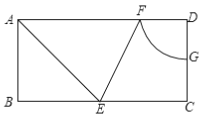
查看答案和解析>>【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )

A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A在数轴上位于原点的左侧,距离原点3个单位长度,若将点A向右移动4个单位长度,再向左移动2个单位长度,此时点A表示的数是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)△BEF是等腰三角形吗?试说明理由;
(2)若AB=4,AD=8,求CF的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若
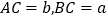 ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:(1)试说明
 ;
;(2)如果大正方形的面积是10,小正方形的面积是2,求
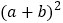 的值.
的值.
相关试题

