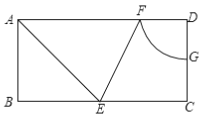
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
参考答案:
【答案】![]()
【解析】试题分析:先由矩形的性质得出,∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,根据AE平分∠BAD得到∠BAE=∠EAD=45°,那么△ABE是等腰直角三角形,于是AB=BE=2,AE=![]() AB=2
AB=2![]() .再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2
.再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2![]() ,DF=AD-AF=4-2
,DF=AD-AF=4-2![]() ,然后根据弧长的计算公式即可求出
,然后根据弧长的计算公式即可求出![]() 的长.
的长.
试题解析:∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,
∵AE平分∠BAD交边BC于点E,
∴∠BAE=∠EAD=45°,
∴△ABE是等腰直角三角形,
∴AB=BE=2,AE=![]() AB=2
AB=2![]()
∵∠AEC的分线交AD于点F,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,
∴AF=AE=2![]()
∴DF=AD-AF=4-2![]()
∴![]() 的长为:
的长为: 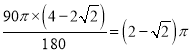 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂生产的一种巧克力糖每千克成本为24元,其销售方案有如下两种:
方案一:若直接给本厂设在银川的门市部销售,则每千克售价为32元,但门市部每月需上缴有关费用2400元;
方案二:若直接批发给本地超市销售,则出厂价为每千克28元.若每月只能按一种方案销售,且每种方案都能按月销售完当月产品,设该厂每月的销售量为xkg.
(1)你若是厂长,应如何选择销售方案,可使工厂当月所获利润更大?
(2)厂长看到会计送来的第一季度销售量与利润关系的报表后(下表),发现该表填写的销售量与实际有不符之处,请找出不符之处,并计算第一季度的实际销售总量.
一月
二月
三月
销售量(kg)
550
600
1400
利润(元)
2000
2400
5600
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的说法正确的是( )
A.有理数的绝对值一定比0大
B.有理数的相反数一定比0小
C.如果两个数的绝对值相等,那么这两个数相等
D.互为相反数的两个数的绝对值相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B的坐标分别为A(-4,0)、B(2,0),点C在y轴上,且△ABC的面积为6,以点A、B、C为顶点作□ABCD.若过原点的直线平分该□ABCD的面积,则此直线的解析式是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )

A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A在数轴上位于原点的左侧,距离原点3个单位长度,若将点A向右移动4个单位长度,再向左移动2个单位长度,此时点A表示的数是___.
相关试题

