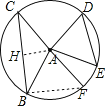
【题目】如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.

参考答案:
【答案】3.
【解析】
试题分析:作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=![]() BF=3.
BF=3.
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴![]() =
=![]() ,
,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=![]() BF=3.
BF=3.
∴点A到弦BC的距离为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形的一个外角等于40°,则这个多边形的边数是( )
A. 6 B. 9 C. 12 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
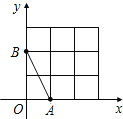
(1)求线段AB所在直线的函数解析式;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,指定位置画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而 (填“增大”或“减小”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=﹣
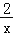 与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.
与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.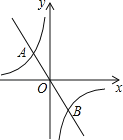
(1)求正比例函数的表达式及点B的坐标;
(2)结合图象直接写出当kx>﹣
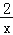 时,x的取值范围是 .
时,x的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程﹣3x2=5(x﹣3)的二次项系数是 , 常数项是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.三角形两边之和大于第三边
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,4)与点B(3,y)关于y轴对称,那么x+y的值为____________.
相关试题

