【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.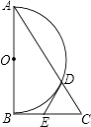
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
参考答案:
【答案】
(1)证明:连接OD,OE,BD, 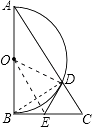
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
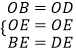 ,
,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
∴OD⊥DE
则DE为圆O的切线;
(2)解:在Rt△ABC中,∠BAC=30°,
∴BC= ![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.
【解析】(1)方法一、要证明DE是半圆⊙O的切线.由已知可知点D在半圆上,因此连接半径OD,再证明OD⊥DE,还需连接OE,BD, 根据直角三角形斜边上的中线等于斜边的一半,证得DE=BE,从而可证明△OBE≌△ODE,得出∠ODE=∠ABC=90°,即可证得结论;方法二、或先证DE=BE,得出∠BDE=∠DBE,再由OB=OD得出∠OBD=∠ODB,而∠ABC=90°=∠OBD+∠DBE,继而可知∠BDE+∠ODB=90°,得出OD⊥DE,即可证得结论。
(2)由已知易求出BC的长,再由直角三角形中,30°角所对的直角边等于斜边的一半,可求出AC的长,再证明△DEC为等边三角形,从而可求得结果。
【考点精析】掌握含30度角的直角三角形和直角三角形斜边上的中线是解答本题的根本,需要知道在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半.
-
科目: 来源: 题型:
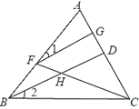
查看答案和解析>>【题目】如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.
(1)说明:∠1=∠2.
(2)若∠A=80°,FG⊥AC,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里装有8个红球,4个黄球,3个白球,他们除了颜色外都相同,两人做游戏,游戏规则如下:一个人抓住袋子,一个人摸球,若摸出红球,摸球者胜,否则拿袋子的人获胜.
(1)如果你参加游戏,为了尽可能的获胜,你是做摸球的人还是做拿袋子的人?为什么?
(2)你说这个游戏公平吗?如果公平,说明理由:如果不公平,请给出修改建议,使它对双方都是公平的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
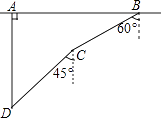
-
科目: 来源: 题型:
查看答案和解析>>【题目】永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣
 x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).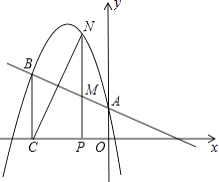
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
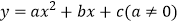 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:① 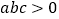 ;②
;② 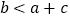 ;③
;③ 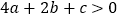 ;④
;④  ; ⑤
; ⑤ 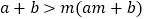 ,(
,( 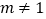 的实数)其中正确的结论有( )
的实数)其中正确的结论有( )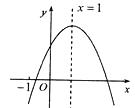
A.2个
B.3个
C.4个
D.5个
相关试题

