【题目】永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
参考答案:
【答案】
(1)解:w=(x﹣18)y=(x﹣18)(﹣2x+100)
=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800(x>18)
(2)解:∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴当x=34时,w取得最大,最大利润为512万元.
答:当销售单价为34元时,厂商每周能获得最大利润,最大利润是512万元.
(3)解:周销售利润=周销量×(单件售价﹣单件制造成本)=(﹣2x+100)(x﹣18)=﹣2x2+136x﹣1800,
由题意得,﹣2x2+136x﹣1800=350,
解得:x1=25,x2=43,
∵销售单价不得高于30元,
∴x取25,
答:销售单价定为25元时厂商每周能获得350万元的利润;
【解析】(1)根据利润w=(每盏节能灯的售价-每盏节能灯的进价)![]() 每周的销量y,即可求出函数解析式。
每周的销量y,即可求出函数解析式。
(2)将(1)中的函数解析式通过配方,求出其顶点坐标,即可得出结果。
(3)此小题的等量关系是:每周获得的利润w=350,建立方程求解即可。注意:0<x≤30.
【考点精析】本题主要考查了因式分解法和二次函数的最值的相关知识点,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子里装有8个红球,4个黄球,3个白球,他们除了颜色外都相同,两人做游戏,游戏规则如下:一个人抓住袋子,一个人摸球,若摸出红球,摸球者胜,否则拿袋子的人获胜.
(1)如果你参加游戏,为了尽可能的获胜,你是做摸球的人还是做拿袋子的人?为什么?
(2)你说这个游戏公平吗?如果公平,说明理由:如果不公平,请给出修改建议,使它对双方都是公平的.
-
科目: 来源: 题型:
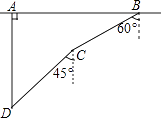
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
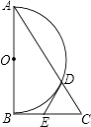
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣
 x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).
x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x轴,垂足为点C(﹣3,0).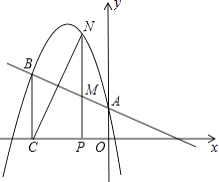
(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(3)在(2)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
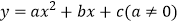 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:① 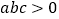 ;②
;② 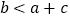 ;③
;③ 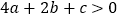 ;④
;④  ; ⑤
; ⑤ 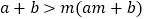 ,(
,( 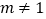 的实数)其中正确的结论有( )
的实数)其中正确的结论有( )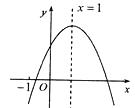
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】位于红星路济宁师专旧址的济宁学院附中红星校区将于近期开始动工,原计划在年内拆除旧校舍与建造新校舍共12万平方米,为建设一座园林式的校园,在实施中调整拆建计划,新建面积减少10%,拆除面积增加10%,结果拆除和新建总面积不变.根据协议,施工方免费拆除旧校舍,但建造新校舍每平米需要1500元,校园环境建设每平方米需要600元.
(1)求原计划拆、建的面积各多少平方米?
(2)若把实际的拆、建工程中节余的资金的30%用来增加校园环境建设,可建设多少平方米?
相关试题

