【题目】在数轴上,![]() 为原点,点
为原点,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() .
.
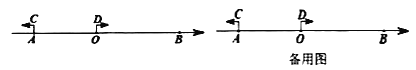
(1)求线段![]() 的长;
的长;
(2)如图,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿数轴向左匀速运动,动点
出发,以每秒1个单位的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿数轴向右匀速运动.
个单位的速度沿数轴向右匀速运动.![]() 、
、![]() 两点同时出发,运动时间为
两点同时出发,运动时间为![]() .
.
(i)当![]() 时,求运动时间
时,求运动时间![]() ;
;
(ii)![]() 、
、![]() 、
、![]() 三点中的某一个点是另两个点的中点,求点
三点中的某一个点是另两个点的中点,求点![]() 表示的数
表示的数![]() .
.
参考答案:
【答案】(1)线段![]() 的长为7;(2)(i)运动时间
的长为7;(2)(i)运动时间![]() 为
为![]() 秒或8秒;(ii)点
秒或8秒;(ii)点![]() 表示的数
表示的数![]() 为-
为-![]() 或-
或-![]()
【解析】
(1)由![]() 可得a=-3,b=4,由b-a可得线段
可得a=-3,b=4,由b-a可得线段![]() 的长;
的长;
(2)由题意可得AC=t,OD=![]() t,(i)分点D在点B左侧和右侧两种情况讨论即可;(ii)分点D在点B左侧时CD=BD和点D在点B右侧时BC=BD两种情况讨论即可.
t,(i)分点D在点B左侧和右侧两种情况讨论即可;(ii)分点D在点B左侧时CD=BD和点D在点B右侧时BC=BD两种情况讨论即可.
(1)由![]() ,
,
可得a=-3,b=4,
线段![]() 的长为b-a=4-(-3)=7;
的长为b-a=4-(-3)=7;
(2)由题意可得AC=t,OD=![]() t,OB=4,
t,OB=4,
(i)∵![]() ,
,
∴BD=2t,
当点D在点B左侧时,如图:
![]()
此时OD+BD=OB,即![]() t+2t=4,解得t=
t+2t=4,解得t=![]() ;
;
当点D在点B右侧时,如图:
![]()
此时OB+BD=OD,即4+2t=![]() t,解得t=8;
t,解得t=8;
故运动时间![]() 为
为![]() 秒或8秒;
秒或8秒;
(ii)如图:
![]()
当点D在点B左侧时,点D为BC的中点,
此时CD=BD,
即3+t+![]() t=4-
t=4-![]() t,
t,
解得t=![]() ,
,
此时c=-3-![]() =-
=-![]() ;
;
如图:
![]()
当点D在点B右侧时,点B为CD的中点,
此时BC=BD,
即3+4+t=![]() t-4,
t-4,
解得t=![]() ,
,
此时c=-3-![]() =-
=-![]() ,
,
综上,点![]() 表示的数
表示的数![]() 为-
为-![]() 或-
或-![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE、CD 相交于点 A,连接 BC,DE,下列条件中不能判断△ABC∽ADE 的是( )
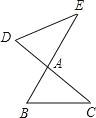
A. ∠B=∠D B. ∠C=∠E C.
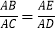 D.
D. 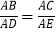
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于整式
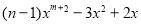 (其中m是大于
(其中m是大于 的整数).
的整数).(1)若
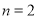 ,且该整式是关于x的三次三项式,求m的值;
,且该整式是关于x的三次三项式,求m的值;(2)若该整式是关于x的二次单项式,求m,n的值;
(3)若该整式是关于x的二次二项式,则m,n要满足什么条件?
-
科目: 来源: 题型:
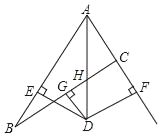
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)求证:AE=AF;
(2)求证:BE=CF;
(3)如果AB=12,AC=8,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,要求每件销售价格不得高于27元,并将所得利润捐给贫困母亲。经试验发现,若每件按22元的价格销售时,每天能卖出42件;若每件按25元的价格销售时,每天能卖出33件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润
 最大,最大利润是多少?
最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期第三周周末,七年级27班在人美心善的范老师的带领下开展了大型“绿水青山都是金山银山”的植树活动.全班一起种植许愿树和发财树.已知购买1棵许愿树和2棵发财树需要42元,购买2棵许愿树和1棵发财树需要48元.
(1)你来算一算许愿树、发财树每棵各多少钱?
(2)范老师传达最高指示:全班种植许原树和发财树共20棵,且许愿树的数量不少于发财树的数量,但由于班费资金紧张,范老师还要求两种树的总成本不得高于312元.聪明的同学们,你们知道共有哪几种种植方案吗?
-
科目: 来源: 题型:
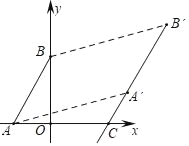
查看答案和解析>>【题目】如图,已知A(﹣2,0),B(0,4),将线段AB平移到第一象限得线段A′B′,点A′的横坐标为5,若作直线A′B′交x轴于点C(4,0).
(1)求线段AB所在直线的解析式;
(2)直线AB上一点P(m,n),求出m、n之间的数量关系;
(3)若点Q在y轴上,求QA′+QB′的取值范围.
相关试题

