【题目】本学期第三周周末,七年级27班在人美心善的范老师的带领下开展了大型“绿水青山都是金山银山”的植树活动.全班一起种植许愿树和发财树.已知购买1棵许愿树和2棵发财树需要42元,购买2棵许愿树和1棵发财树需要48元.
(1)你来算一算许愿树、发财树每棵各多少钱?
(2)范老师传达最高指示:全班种植许原树和发财树共20棵,且许愿树的数量不少于发财树的数量,但由于班费资金紧张,范老师还要求两种树的总成本不得高于312元.聪明的同学们,你们知道共有哪几种种植方案吗?
参考答案:
【答案】(1)许愿树、发财树每棵各18元,12元;(2)见解析.
【解析】
(1)设许愿树每棵x元,发财树每棵y元,根据“购买1棵许愿树和2棵发财树需要42元,购买2棵许愿树和1棵发财树需要48元”列出方程组并解答;
(2)设许愿树为a棵,则发财树为(20-a)棵,根据“两种树的总成本不得高于312元且许愿树的数量不少于发财树的数量”列出不等式组并求得a的取值范围,进行解答.
(1)设许愿树每棵x元,发财树每棵y元,根据题意可得:
![]() ,
,
解得:![]() ,
,
答:许愿树、发财树每棵各18元,12元;
(2)设许愿树为a棵,则发财树为(20-a)棵,根据题意可得:
![]() ,
,
解得:10≤a≤12,
∴a=10,11,12;
所以有三种方案,方案一,10棵许愿树、10棵发财树;
方案二,11棵许愿树、9棵发财树;
方案三,12棵许愿树、8棵发财树.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
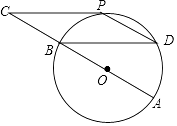
(1)求证:点P为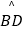 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.
(1)求自行车和书包单价各为多少元;
(2)新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
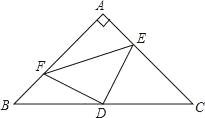
查看答案和解析>>【题目】已知:如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.若BC=8,则四边形AFDE的面积是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
有一些相同的房间需要粉刷,一天 3名一级技工去粉刷 8个房间,结果其中有 50
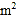 墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40
墙面未来得及刷;同样时间内 5名二级技工粉刷了 10个房间之外,还多刷了另外的40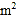 墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10
墙面.已知每名同级别的技工每天的工作效率相同,每名一级技工比二级技工每天多刷 10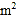 墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?
墙面,求每个一级技工和二级技工每天粉刷的墙面各是多少平方米?
相关试题

