【题目】如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2﹣7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为![]() 时运动时间t的值;
时运动时间t的值;
(3)当点P运动到边AC上时,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

参考答案:
【答案】(1) AB=3,BC=4;(2) t=4;(3) t为10秒或9.5秒或![]() 秒时,△CDP是等腰三角形.
秒时,△CDP是等腰三角形.
【解析】试题分析:(1)解一元二次方程即可求得边长;
(2)结合图形,利用勾股定理求解即可;
(3)根据题意,分为:PC=PD,PD=PC,PD=CD,三种情况分别可求解.
试题解析:(1)∵x2-7x+12=(x-3)(x-4)=0
∴![]() =3或
=3或![]() =4 .
=4 .
则AB=3,BC=4
(2)由题意得![]()
∴![]() ,
, ![]() (舍去)
(舍去)
则t=4时,AP=![]() .
.
(3)存在点P,使△CDP是等腰三角形.
①当PC=PD=3时, t=![]() =10(秒).
=10(秒).
②当PD=PC(即P为对角线AC中点)时,AB=3,BC=4.
∴AC=![]() =5,CP1=
=5,CP1= ![]() AC=2.5
AC=2.5
∴t=![]() =9.5(秒)
=9.5(秒)
③当PD=CD=3时,作DQ⊥AC于Q.  ,
, 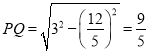
∴PC=2PQ=![]()
∴ (秒)
(秒)
可知当t为10秒或9.5秒或![]() 秒时,△CDP是等腰三角形.
秒时,△CDP是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
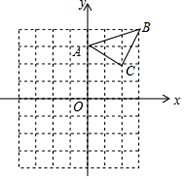
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是( )
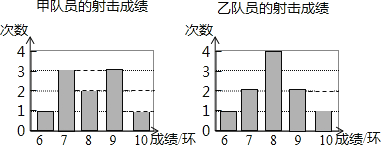
A. 甲队员成绩的平均数比乙队员的大
B. 乙队员成绩的平均数比甲队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 甲队员成绩的方差比乙队员的大
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
 都可以进行这样的分解:
都可以进行这样的分解: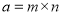 (
(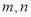 是正整数,且
是正整数,且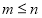 ),在
),在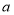 的所有这种分解中,如果
的所有这种分解中,如果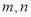 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称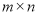 是
是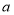 的最佳分解,产规定:
的最佳分解,产规定: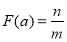 ,例如:12可以分解成
,例如:12可以分解成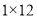 ,
,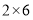 ,
,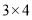 ,因为
,因为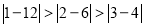 ,所以
,所以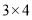 是12的最佳分解,所以
是12的最佳分解,所以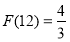 .
.(1)求
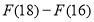 ;
;(2)若正整数
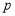 是4的倍数,我们称正整数
是4的倍数,我们称正整数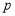 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数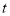 ,
,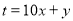 (
(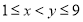 ,
,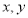 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】百货商店销售某种冰箱,每台进价2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台。(销售利润=销售价—进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为 元,平均每天可销售冰箱 台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):

若规定坐标号(m,n)表示第m行从左向右第n个数,则(7,4)所表示的数是_____;(5,8)与(8,5)表示的两数之积是_______;数2012对应的坐标号是_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

相关试题

