【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
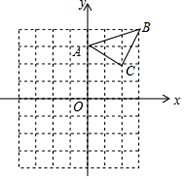
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
参考答案:
【答案】(1)(2,-2);(2)(1,0);(3)10.
【解析】试题分析:(1)将点A、B、C分别向左平移4个单位得到对应点,再顺次连接可得;
(2)利用位似图形的性质得出对应点位置,进而得出答案;
(3)割补法求解可得.
试题解析:
(1)如图,△A1B1C1即为所求,点C1的坐标是(﹣2,2),
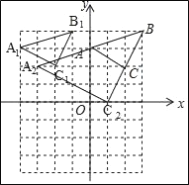
故答案为:(﹣2,2);
(2)如图所示,△A2B2C2即为所求,点C2的坐标是(1,0),
故答案为:(1,0);
(3)△A2B2C2的面积![]() ×(2+4)×6﹣
×(2+4)×6﹣![]() ×2×4﹣
×2×4﹣![]() ×2×4=10,
×2×4=10,
故答案为:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】《山西省新能源汽车产业2018年行动计划》指出,2018年全省新能源汽车产能将达到30万辆,按照“十三五”规划,到2020年,全省新能源汽车产能将达到41万辆,若设这两年全省新能源汽车产能的平均增长率为
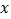 ,则根据题意可列出方程是()
,则根据题意可列出方程是()A.
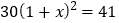 B.
B. 
C.
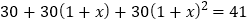 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 于点
于点
(1)如图1,若
 的角平分线交
的角平分线交 于点
于点 ,
, ,
, ,求
,求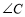 的度数;
的度数;(2)如图2,点
 分别在线段
分别在线段 上,将
上,将 折叠,点
折叠,点 落在点
落在点 处,点
处,点 落在点
落在点 处,折痕分别为
处,折痕分别为 和
和 ,且点
,且点 ,点
,点 均在直线
均在直线 上,若
上,若 ,试猜想
,试猜想 与
与 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;(3)在(2)小题的条件下,将
 绕点
绕点 逆时针旋转一个角度
逆时针旋转一个角度 (
( ),记旋转中的
),记旋转中的 为
为 (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线 与直线
与直线 交于点
交于点 ,直线
,直线 与直线
与直线 交于点
交于点 ,若
,若 ,是否存在这样的
,是否存在这样的 两点,使
两点,使 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋里装有两个白球和一个红球,它们除颜色外其他都一样.
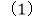 “从袋中任意摸出一个球,摸出的一个球是白球”的概率是______ ;
“从袋中任意摸出一个球,摸出的一个球是白球”的概率是______ ;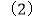 用列表或画树状图的方法求出“从袋中同时任意摸出两个球,摸出的两个球都是白球”的概率.
用列表或画树状图的方法求出“从袋中同时任意摸出两个球,摸出的两个球都是白球”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩,根据统计图中的信息,下列结论正确的是( )
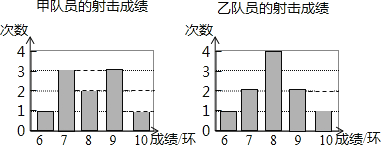
A. 甲队员成绩的平均数比乙队员的大
B. 乙队员成绩的平均数比甲队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 甲队员成绩的方差比乙队员的大
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数
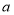 都可以进行这样的分解:
都可以进行这样的分解: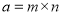 (
(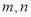 是正整数,且
是正整数,且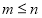 ),在
),在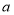 的所有这种分解中,如果
的所有这种分解中,如果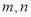 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称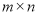 是
是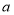 的最佳分解,产规定:
的最佳分解,产规定: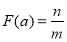 ,例如:12可以分解成
,例如:12可以分解成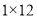 ,
,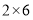 ,
,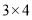 ,因为
,因为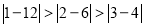 ,所以
,所以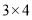 是12的最佳分解,所以
是12的最佳分解,所以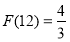 .
.(1)求
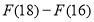 ;
;(2)若正整数
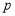 是4的倍数,我们称正整数
是4的倍数,我们称正整数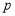 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数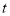 ,
,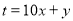 (
(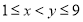 ,
,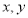 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数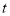 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中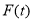 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,边AB、BC的长(AB<BC)是方程x2﹣7x+12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒).
(1)求AB与BC的长;
(2)当点P运动到边BC上时,试求出使AP长为
 时运动时间t的值;
时运动时间t的值;(3)当点P运动到边AC上时,是否存在点P,使△CDP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.

相关试题

