【题目】甲乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,两人同时起跑.
(1)两人出发后多长时间乙追上甲?
(2)求从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数关系,并画出y(m)与时间t(s)的图象.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,画图见解析.
,画图见解析.
【解析】
(1)根据题意列式计算即可解答;
(2)甲在乙前面,而乙的速度大于甲,则此过程为乙先追上甲后再超过甲,全程时间为乙跑的时间,算出相遇时间,画出图象.
解:(1)100÷(6﹣4)=50s.
故两人出发后50s乙追上甲;
(2)当t≤50时,
![]() ,
,
∴![]()
当50<t≤200时,
![]()
∴![]()
全程乙跑完后计时结束:t总=![]() s,
s,
则计时结束后甲乙的距离:s=(6﹣4)×(200﹣50)=300m,
故甲、乙两之间的距离y(m)与时间t(s)的函数图象如图所示:
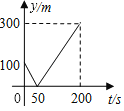
-
科目: 来源: 题型:
查看答案和解析>>【题目】用1块A型钢板可制成2块C型钢板和1块D型钢板;用1块B型钢板可制成1块C型钢板和3块D型钢板.现准备购买A、B型钢板共100块,并全部加工成C、D型钢板.要求C型钢板不少于120块,D型钢板不少于250块,设购买A型钢板x块(x为整数).
(1)求A、B型钢板的购买方案共有多少种?
(2)出售C型钢板每块利润为100元,D型钢板每块利润为120元.若将C、D型钢板全部出售,请你设计获利最大的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂前5个月生产的总产量y(件)与时间x(月)的关系如图所示,则下列说法正确的是( )
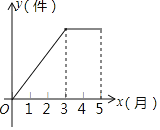
A. 1﹣3月的月产量逐月增加,4、5两月产量逐月减少
B. 1﹣3月的月产量逐月增加,4、5两月产量与3月持平
C. 1﹣3月的月产量逐月增加,4、5两月停产
D. 1﹣3月的月产量逐月持平,4、5两月停产
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )度.
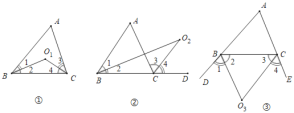
A. 84B. 111C. 225D. 201
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
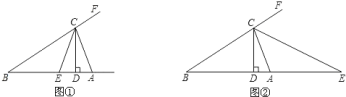
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA是⊙O的切线,A是切点,AC是直径,AB是弦,连接PB、PC,PC交AB于点E,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)若∠APC=3∠BPC,求
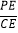 的值.
的值.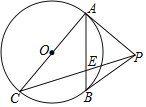
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”
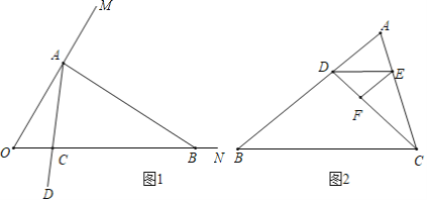
概念理解:如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)
(1)∠ABO的度数为______,△AOB______(填“是”或“不是”)“和谐三角形”;
(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.
应用拓展:(3)如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.
相关试题

