【题目】如图1,点![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足
满足![]() ,将点
,将点![]() 、
、![]() 分别向上平移2个单位,再向右平移1个单位至
分别向上平移2个单位,再向右平移1个单位至![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)直接写出点![]() 的坐标:__________;
的坐标:__________;
(2)连接![]() 交
交![]() 于一点
于一点![]() ,求
,求![]() 的值:
的值:
(3)如图2,点![]() 从
从![]() 点出发,以每秒1个单位的速度向上平移运动,同时点
点出发,以每秒1个单位的速度向上平移运动,同时点![]() 从
从![]() 点出发,以每秒2个单位的速度向左平移运动,设射线
点出发,以每秒2个单位的速度向左平移运动,设射线![]() 交
交![]() 轴于
轴于![]() .问
.问![]() 的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
的值是否为定值?如果是定值,请求出它的值;如果不是定值,请说明理由.
参考答案:
【答案】解:(1)![]() ;(2)
;(2)![]() ;(3)证明略;
;(3)证明略;
【解析】
(1)利用非负数的性质,构建方程组即可解决问题.
(2)利用平行线分线段成比例定理即可解决问题.
(3)结论:S△FMD-S△OFN的值是定值.分两种情形:如图2-1中,当点N在线段OB上时,连接OD.如图2-2中,当点N在BO的延长线上时,连接OD.分别说明即可解决问题.
(1)∵![]() ,
,
又∵(3a+b)2≥0,b-a-4≥0,
∴![]() ,
,
解得![]() ,
,
∴A(-1,0),B(3,0),
∴AB=CD=4,
∵OC=2,CD∥AB,
∴D(4,2),
故答案为(4,2).
(2)如图1中,
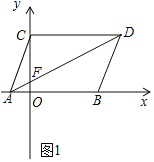
∵CD∥OA,
∴![]() ,
,
∵CD=4,OA=1,
∴![]()
(3)结论:S△FMD-S△OFN的值是定值.
理由:如图2-1中,当点N在线段OB上时,连接OD.
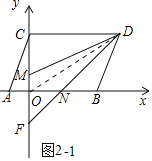
由题意:OM=t,BN=2t,
∴S△OMD=![]() ×t×4=2t,S△DBN=
×t×4=2t,S△DBN=![]() ×2t×2=2t,
×2t×2=2t,
∴S△OMD=S△BND,
∴S四边形DMON=S△OBD=![]() ×3×2=3,
×3×2=3,
∵S△FMD-S△OFN=S四边形DMON=3=定值.
如图2-2中,当点N在BO的延长线上时,连接OD.
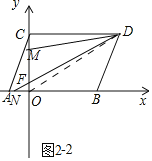
∵S△FMD-S△OFN=S△ODM-S△ODN=S△DBN-S△ODN=S△OBD=3=定值,
综上所述,S△FMD-S△OFN的值是定值,定值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分6分)一只不透明的袋子中装有1个白球、1个蓝球和2个红球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,摸出红球的概率为 ;
(2)从袋中随机摸出1个球(不放回)后,再从袋中余下的3个球中随机摸出1个球,球两次摸到的球颜色不相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为1的正
 的顶点
的顶点 在原点,点
在原点,点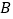 在
在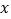 轴负半轴上,正方形
轴负半轴上,正方形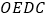 边长为2,点
边长为2,点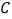 在
在 轴正半轴上,动点
轴正半轴上,动点 从点
从点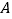 出发,以每秒1个单位的速度沿着
出发,以每秒1个单位的速度沿着 的边按逆时针方向运动,动点
的边按逆时针方向运动,动点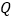 从
从 点出发,以每秒1个单位的速度沿着正方形
点出发,以每秒1个单位的速度沿着正方形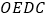 的边也按逆时针方向运动,点
的边也按逆时针方向运动,点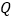 比点
比点 迟1秒出发,则点
迟1秒出发,则点 运动2016秒后,则
运动2016秒后,则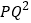 的值是___________.
的值是___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知正方形ABCD,点A(2,0),B(0,4),那么点C的坐标是___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个构造完全相同(除所标数字外)的转盘A、B.
(1)单独转动A盘,指向奇数的概率是 ;
(2)小红和小明做了一个游戏,游戏规定,转动两个转盘各一次,两次转动后指针指向的数字之和为奇数则小红获胜,数字之和为偶数则小明获胜,请用树状图或列表说明谁获胜的可能性大.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

相关试题

