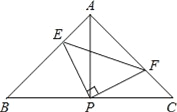
【题目】如图已知在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB和AC于点E、F,给出以下五个结论正确的个数有( )
①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),S四边形AEPF=![]() S△ABC.
S△ABC.
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】D
【解析】试题分析:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴AP⊥BC,AP=PC,∠EAP=∠C=45°,
∴∠APF+∠CPF=90°,
∵∠EPF是直角,
∴∠APF+∠APE=90°,
∴∠APE=∠CPF,故②正确;
在△APE和△CPF中,
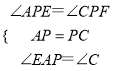 ,
,
∴△APE≌△CPF(ASA),
∴AE=CF,故①正确;
∵△AEP≌△CFP,同理可证△APF≌△BPE,故③正确;
∴△EFP是等腰直角三角形,故④正确;
∵△APE≌△CPF,
∴S△APE=S△CPF,
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=![]() S△ABC,故⑤正确.
S△ABC,故⑤正确.
综上所述,正确的结论有①②③④⑤共5个.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知
 、
、 两组发言人数的比为
两组发言人数的比为 ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:组别
发言次数



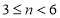


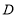


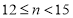

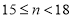

(1)求出样本容量,并补全条形统计图;
(2)求
 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.

-
科目: 来源: 题型:
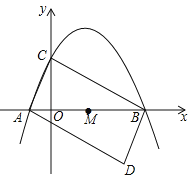
查看答案和解析>>【题目】如图,抛物线y=﹣
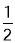 x2+
x2+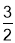 x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.3
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边 且BE=CF,AD+EC=AB.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数.
-
科目: 来源: 题型:
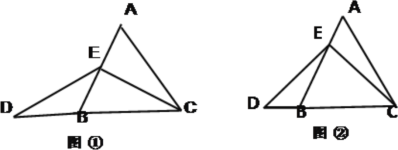
查看答案和解析>>【题目】在等边△ABC中,点E在AB上,点D在CB延长线上,且ED=EC.
(1)当点E为AB中点时,如图①,AE DB(填“﹥”“﹤”或“=”),并说明理由;
(2)当点E为AB上任意一点时,如图②,AE DB(填“﹥”“﹤”或“=”),并说明理由;(提示:过点E作EF∥BC,交AC于点F)
(3)在等边△ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,请你画出图形,并直接写出相应的CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄山位于安徽省南部,是世界文化与自然双重遗产,世界地质公园,国家
 级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.暑假期间,太和县某学校组织七年级学生到黄山游学,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该学校七年级有303名学生参加这次游学活动,学校计划每辆车安排一名老师,老师也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助学校设计租车方案.
②旅行前,学校的一名老师由于特殊情况,学校只能安排7名老师,为保证所租的每辆车均有一名老师,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问学校的租车方案如何安排?
相关试题

