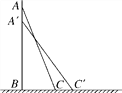
【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?
参考答案:
【答案】(1)这个梯子的顶端距地面有2.4米;(2)梯子的底端在水平方向滑动了0.8米.
【解析】试题分析:(1)、根据Rt△ABC的勾股定理求出AB的长度,从而得出答案;(2)、根据题意得出A`C`和A`B的长度,然后根据勾股定理求出BC`的长度,从而得出答案.
试题解析:(1)、根据题意可得:AC=2.5米,BC=0.7米,∠ABC=90°,
∴AB=![]() 米,即梯子的顶端距地面有2.4米;
米,即梯子的顶端距地面有2.4米;
(2)、根据题意可得:A`C`=2.5米,A`B=2.4-0.4=2米,
∴BC`=![]() 米,则CC`=1.5-0.7=0.8米,即梯子的底端在水平方向滑动0.8米.
米,则CC`=1.5-0.7=0.8米,即梯子的底端在水平方向滑动0.8米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
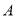 在
在 轴正半轴上,点
轴正半轴上,点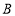 在
在 轴正半轴上连接
轴正半轴上连接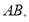
 的长为
的长为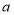 ,其中
,其中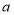 是不等式
是不等式 的最大整数解
的最大整数解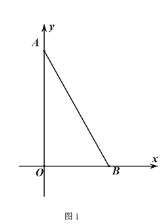
(1)求
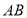 的长
的长(2)动点
 以每秒
以每秒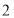 个单位长度的速度在
个单位长度的速度在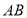 上从
上从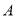 点向
点向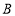 点运动,设
点运动,设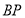 的长度为
的长度为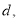 运动时间为
运动时间为 ,请用含
,请用含 的式子表示
的式子表示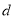 ;
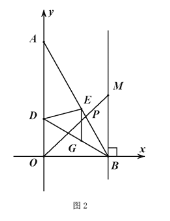
;(3)如图2,在(2)的条件的下,
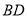 平分
平分 交
交 轴于点
轴于点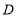 ,点
,点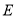 在
在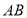 上,点
上,点 在
在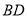 上,连接
上,连接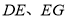 ,且
,且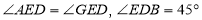 ,点
,点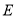 与点
与点 的纵坐标的差为
的纵坐标的差为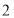 ,连接
,连接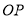 并还延长交过
并还延长交过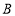 点且与
点且与 轴垂直的直线于
轴垂直的直线于 ,当
,当 为何值时,
为何值时,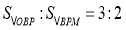 ,并求
,并求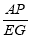 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
参考数据:tan58°≈1.60,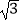 ≈1.732,供选用.
≈1.732,供选用.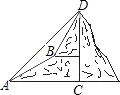
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由. -
科目: 来源: 题型:
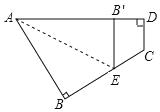
查看答案和解析>>【题目】如图所示,一个四边形纸片 ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点 B 落在 AD 边上的 B′点,AE 是折痕.
(1)试判断 B′E 与 DC 的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 .

(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
相关试题

