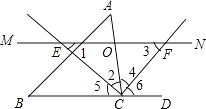
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
参考答案:
【答案】
(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF= ![]() =13,
=13,
∴OC= ![]() EF=6.5
EF=6.5
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
【解析】(1)根据角平分线的定义得到角相等,再由平行线的性质得到内错角相等,由等角对等边得到EO=CO,FO=CO,即OE=OF;(2)由互为邻补角的平分线互相垂直得到∠2+∠4=∠5+∠6=90°,根据勾股定理得到EF=13,求出OC的值;(3)根据矩形的判定方法可知,当O为AC的中点时得到四边形AECF是平行四边形,再由有一个角是直角的平行四边形是矩形判定即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲乙两数学兴趣小组测量出CD的高度,甲小组在地面A处测量,乙小组在上坡B处测量,AB=200m,甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D的仰角为58°,求山CD的高度(结果保留一位小数)
参考数据:tan58°≈1.60,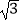 ≈1.732,供选用.
≈1.732,供选用.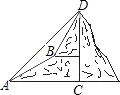
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
-
科目: 来源: 题型:
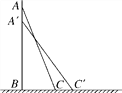
查看答案和解析>>【题目】如图,一架梯子AC长2.5米,斜靠在一面墙上,梯子底端离墙0.7米.
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了0.4米到A′,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
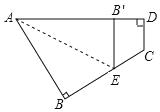
查看答案和解析>>【题目】如图所示,一个四边形纸片 ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点 B 落在 AD 边上的 B′点,AE 是折痕.
(1)试判断 B′E 与 DC 的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 .

(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,D、E、F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C.
(1)求证:DE∥BC;
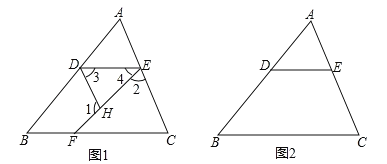
(2)在以上条件下,若△ABC及D,E两点的位置不变,点F在边BC上运动使得∠DEF的大小发生变化,保证点H存在且不与点F重合,探究:要使∠1=∠BFH成立,请说明点F应该满足的位置条件,在图2中画出符合条件的图形并说明理由.
(3)在(2)的条件下,若∠C=α,直接写出∠BFH的大小 .
相关试题

