Question

【题目】某公司投资1200万元购买了一条新生产线生产新产品．根据市场调研，生产每件产品需要成本50元，该产品进入市场后不得低于80元/件且不得超过160元/件，该产品销售量y（万件）与产品售价x（元）之间的关系如图所示．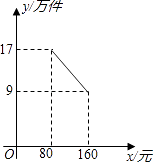
（1）求y与x之间的函数关系式，并写出x的取值范围；
（2）第一年公司是盈利还是亏损？求出当盈利最大或亏损最小时的产品售价；
（3）在（2）的前提下，即在第一年盈利最大或者亏损最小时，公司第二年重新确定产品售价，能否使前两年盈利总额达790万元？若能，求出第二年产品售价；若不能，说明理由．

Answer 1

【答案】
（1）解：设y=kx+b．由图象可得： ，

解得： ．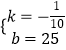

所以y=﹣ x+25，

故x的取值范围是80≤x≤160

（2）解：设该公司第一年获利S万元，则

S=（x﹣50）×y﹣1200=（x﹣50）（﹣ x+25）﹣1200

=﹣ x2+30x﹣2450

=﹣ （x﹣150）2﹣200≤﹣200，

所以第一年公司是亏损，且当亏损最小时的产品售价为150元/件

（3）解：由题意可列方程（x﹣50）（﹣ x+25）+（﹣200）=790，

解得：x1=140，x2=160．

两个x的值都在80≤x≤160内，

所以第二年售价是140元/件或160/件

【解析】（1）设y=kx+b，则由图象可求得k，b，从而得出y与x之间的函数关系式，并写出x的取值范围80≤x≤160；（2）设公司第一年获利S万元，则可表示出S=﹣ （x﹣150）2﹣200≤﹣200，则第一年公司亏损了，当产品售价定为150元/件时，亏损最小，最小亏损为200万元；（3）假设两年共盈利790万元，则（x﹣50）（﹣ x+25）+（﹣200）=790，解得x的值在80≤x≤160内．