【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .
参考答案:
【答案】5.5,或0.5
【解析】解:分两种情况:①如图1所示: 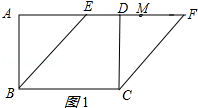
∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=5,∠ADC=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF= ![]() =
= ![]() =3,
=3,
∴AF=AD+DF=8,
∵M是EF的中点,
∴MF= ![]() EF=2.5,
EF=2.5,
∴AM=AF﹣DF=8﹣2.5=5.5;
②如图2所示:同①得:AE=3,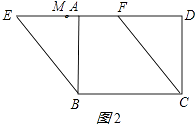
∵M是EF的中点,
∴ME=2.5,
∴AM=AE﹣ME=0.5;
综上所述:线段AM的长为:5.5,或0.5;
故答案为:5.5,或0.5.
两种情况:①由矩形的性质得出CD=AB=4,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=3,求出ME,即可得出AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=
 的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
A.20
B.22
C.24
D.26 -
科目: 来源: 题型:
查看答案和解析>>【题目】王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).

【1】【1】(1)小强让爷爷先上多少米?
【2】【2】(2)山顶离山脚的距离有多少米?谁先爬上山顶?
【3】【3】(3)小强经过多少时间追上爷爷?
-
科目: 来源: 题型:
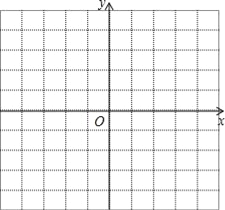
查看答案和解析>>【题目】如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,分别得到A1、B1、C1,依次连接A1,B1,C1,各点,请写出A1、B1、C1的坐标并画出△A1B1C1,并判断所得三角形A1B1C1与三角形ABC的大小、形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,分别得到A2、B2、C2,依次连接A2,B2,C2,各点,请写出A2、B2、C2的坐标并画出△A2B2C2,并判断所得三角形A2B2C2与三角形ABC的大小、形状和位置有什么关系?
(3)求△A2B2C2的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=y,则下列各式①x﹣3=y﹣3,②4x=6y,③﹣2x=﹣2y,④
 ,⑤
,⑤ ,⑥
,⑥ ,其中正确的有( )
,其中正确的有( )A. ①②③ B. ④⑤⑥ C. ①③⑤ D. ②④⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各式分解因式:
(1)
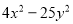 (2)
(2) 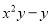
(3)
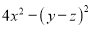 (4)
(4)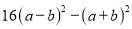
(5)
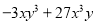 (6)
(6) 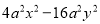
(7)
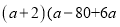 (8)
(8) 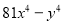
(9)
 (10)
(10) 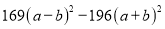
相关试题

